„Spline. Funcții finite. Concepte de bază, scop. În splinele Schoenberg »
Funcții similare cu cele denumite acum spline au fost cunoscute de matematicieni de mult timp în urmă, începând cel puțin cu Euler, dar studiul lor intensiv a început, de fapt, numai la mijlocul secolului al XX-lea. În 1946, Isaac Schoenberg a folosit mai întâi acest termen ca desemnare pentru clasa de spline polinomiale. Până în anii 1960, splinele erau practic un instrument de cercetare teoretică, adesea au apărut ca soluții la diferite probleme extreme și variaționale, în special în teoria aproximării.
După 1960, odată cu dezvoltarea tehnologiei computerizate, a început utilizarea splinelor în grafica și modelarea computerelor, care continuă până în prezent.
Un spline este de obicei înțeles ca o funcție definită în parte care coincide cu funcțiile unei naturi mai simple pe fiecare element al partiției domeniului său de definiție.
Un spline clasic al unei variabile este construit după cum urmează: domeniul definiției este împărțit într-un număr finit de segmente, pe fiecare dintre care spline coincide cu un anumit polinom algebric. Gradul maxim al polinomilor utilizați se numește gradul splinei. Diferența dintre gradul de spline și netezimea rezultată se numește defect spline. De exemplu, o polilinie continuă este o spline de gradul 1 și un defect 1.
Splines au numeroase aplicații atât în teoria matematică, cât și în diferite aplicații de calcul. În particular, splinele a două variabile sunt utilizate intens pentru a defini suprafețele în diferite sisteme de modelare a computerelor.
1.1 Curbe Bezier
Bevierele sau curbele Bernstein-Bezier au fost dezvoltate în anii 60 ai secolului XX independent de Pierre Bezier și Paul de Casteljo.
Curbele au fost prezentate pentru prima dată publicului larg în 1962 de către inginerul francez Pierre Bezier, care, după ce le-a dezvoltat independent de Casteljo, le-a folosit pentru proiectarea computerizată a autovehiculelor. Curbele au fost numite după Beziers, iar numele de Casteljo a denumit metoda recursivă pentru determinarea curbelor (algoritmul lui De Casteljo) dezvoltat de el.
Mai târziu, această descoperire a devenit unul dintre cele mai importante instrumente de sistem de proiectare asistată de calculator și programe de grafică pe calculator.
Curba Bezier este o curbă parametrică dată de expresia:
Este o funcție a componentelor vectorilor de vârf de referință și
, aproximarea primului său derivat
.
Existența unei astfel de teoreme centrale, precum și o serie de teoreme dovedite de Strang-Fix, în special cu privire la existența funcțiilor care satisfac condițiile (2.7), dă un algoritm pentru construirea funcțiilor finite de bază care posedă proprietățile de aproximare necesare.
3. Splinele B din Schoenberg
În matematica computațională, o B-spline este o funcție spline care are cel mai mic purtător pentru un anumit grad, ordinea de netezime și împărțirea domeniului de definiție. Teorema fundamentală stabilește că orice funcție spline pentru un anumit grad, netedă și domeniu de definiție poate fi reprezentată ca o combinație liniară de spline B de același grad și neteditate în același domeniu de definiție. [1] Termenul B-spline a fost introdus de I. Schoenberg și este o abreviere a expresiei "spline de bază". [2] Splinele B pot fi calculate folosind algoritmul de Bohr, care are stabilitate.
În proiectarea asistată de calculator și în grafica computerizată, termenul B-spline descrie adesea o curbă spline, care este specificată de funcțiile spline exprimate prin combinații liniare de spline B.
Atunci când nodurile sunt echidistant unele de altele, se spune că B-spline este omogen, altfel se numește neomogen.
Atunci când numărul de noduri coincide cu gradul de spline, B-spline degenerează într-o curbă Bezier. Forma funcției de bază este determinată de localizarea nodurilor. Scalarea sau traducerea paralelă a vectorului de referință nu afectează funcția de bază.
Splineul este conținut în corpul convex al punctelor sale de referință.
Splinea de bază a gradului n:
.
Ea nu dispare numai pe intervalul [ti, ti + n + 1], adică:
Cu alte cuvinte, modificarea unui punct de referință afectează numai comportamentul local al curbei, mai degrabă decât cel global, ca în cazul curbelor Bezier.
Funcția de bază poate fi obținută din polinomul Bernstein
B-spline și unele dintre cele mai frecvent utilizate baze
Teorema Strang-Fix indică faptul că dacă funcția finită standard
(2.7), atunci seria (2.4), construită pe baza schimbărilor sale, va avea proprietăți de apropiere apropiate.
Schoenberg a propus o clasă interesantă de funcții satisfăcătoare (2.7). funcție
Un B-spline (Schoenberg) de grad
, dacă transformarea lui Fourier are forma
După cum vedem, funcția (6.8) îndeplinește toate condițiile (6.7).
Baza treptelor
Este destul de simplu să arăți că atunci când
este o aproximare printr-o linie continuă întreruptă având derivați discontinui. Apropierea prin norme
are oa doua ordine, conform normei
- primul. Această aproximare este utilizată cel mai adesea pentru rezolvarea ecuațiilor diferențiale de ordinul doi prin metoda de proiecție. Aceasta conduce la cele mai simple formule pentru integrale și la matricea maximă redusă în calcularea acesteia.
Mai mult, această bază, având în vedere faptul că p = 1, are o caracteristică - pentru ca funcția să fie aproximată
coincid cu valorile funcției la nodurile rețelei
, care ne permite să găsim rapid aproximările inițiale pentru
.
este o spline cubică polinomială în bucăți, obținută prin convoluție:
.
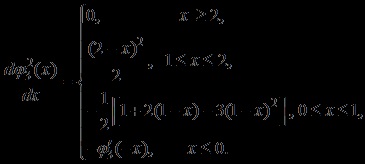
Dimensiunea media la
a crescut la patru (
). Rețineți că pentru a asigura continuitatea celui de-al doilea derivat la puncte
. Așa cum am menționat deja, aproximarea în normă
are a patra ordine, în normă
5. Alberg J. Nilsson E. Walsh J. - Teoria splinelor și a aplicațiilor acestora
Articole similare
Trimiteți-le prietenilor: