Reamintim definiția centrală - definiția logaritmului. Este conectat cu soluția ecuației exponențiale. Această ecuație are o singură rădăcină, se numește logaritmul b al bazei a:
Logaritmul numărului b pe baza a este exponentul la care urmează să fie ridicată baza a pentru a obține numărul b.
Ne amintim identitatea logaritmică de bază.
Expresia (expresia 1) este rădăcina ecuației (expresia 2). Înlocuim valoarea lui x din expresia 1 în locul lui x în expresia 2 și obținem identitatea logaritmică de bază:
Așa că vedem că fiecărei valori i se atribuie o valoare. Noi denotăm b cu x (), c pentru y, și astfel obținem o funcție logaritmică:
Să ne amintim proprietățile de bază ale funcției logaritmice.
Încă o dată, ne acordăm atenție, deoarece sub logaritm poate fi o expresie strict pozitivă, ca bază a logaritmului.
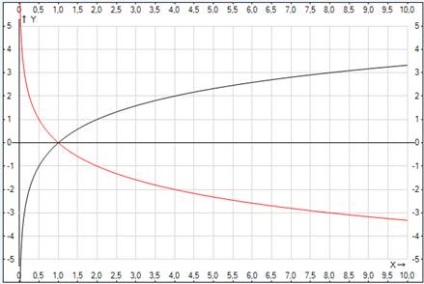
Fig. 1. Graficul funcției logaritmice pentru diferite baze
Graficul funcțiilor este afișat în negru. Fig. 1. Dacă argumentul crește de la zero la infinit, funcția crește de la minus la plus infinit.
Graficul funcțiilor este afișat în roșu. Fig. 1.
Proprietățile acestei funcții:
Funcția este monotonă în întregul domeniu de definiție. Când crește monotonic (strict), o valoare mai mare a funcției corespunde unei valori mai mari a argumentului. Când scade monotonic (strict), o valoare mai mare a argumentului corespunde unei valori mai mici a funcției.
Proprietățile funcției logaritmice sunt cheia rezolvării diferitelor ecuații logaritmice.
Luați în considerare cea mai simplă ecuație logaritmică, toate celelalte ecuații logaritmice, ca regulă, se reduc la o astfel de formă.
Dat fiind că bazele logaritmilor și ale logaritmilor sunt egale, funcțiile sub logaritm sunt de asemenea egale, dar nu trebuie să pierdem din vedere domeniul definirii. Sub logaritm nu poate fi decât un număr pozitiv, avem:
Am constatat că funcțiile f și g sunt egale, prin urmare este suficient să alegem una din orice inegalități pentru a respecta HG.
Astfel, am obținut un sistem mixt în care există o ecuație și o inegalitate:
Inegalitatea, ca regulă, nu este neapărat solvabilă, este suficientă rezolvarea ecuației și înlocuirea rădăcinilor găsite în inegalitate, efectuând astfel un control.
Să formuleze metoda de rezolvare a ecuațiilor logaritmice cele mai simple:
Ecuați baza logaritmilor;
Pentru a echivala funcțiile logaritmice;
Să luăm în considerare exemple specifice.
Exemplul 1 - rezolvarea ecuației:
Bazele logaritmilor sunt inițial egale, avem dreptul de a egala expresiile sublogaritmice, nu uităm de LDZ, vom alege primul logaritm pentru a compila inegalitatea:
Găsim radacina și o înlocuim în inegalitate:
Exemplul 2 - rezolvați ecuația:
Această ecuație diferă de cea anterioară prin aceea că baza logaritmilor este mai mică decât una, dar aceasta nu afectează în nici un fel soluția:
Bazele logaritmilor sunt inițial egale, avem dreptul de a egala expresiile sublogaritmice, nu uităm de LDZ, vom alege al doilea logaritm pentru a compila inegalitatea:
Găsim radacina și o înlocuim în inegalitate:
Avem o inegalitate gresita, ceea ce inseamna ca radacina gasita nu satisface LDU.
Exemplul 3 - rezolvați ecuația:
Bazele logaritmilor sunt inițial egale, avem dreptul de a egala expresiile sublogaritmice, nu uităm de LDZ, vom alege al doilea logaritm pentru a compila inegalitatea:
Găsim radacina și o înlocuim în inegalitate:
Evident, numai prima rădăcină satisface LDU.
Deci, am început să studiem un subiect important - soluția ecuațiilor logaritmice. Am luat în considerare tehnica de rezolvare a ecuațiilor cele mai simple și câteva exemple de aplicare a acesteia.
Articole similare
Trimiteți-le prietenilor: