Vedere generală a monomială
-a este un coeficient care poate aparține oricăror seturi N, Z, Q, R, C
-n este exponentul care aparține setului N
Două monomiale sunt similare dacă au aceeași variabilă și același exponent.
Exemple: 3x2 și -5x2; ½x4 și 2√3x4
Suma monomialelor care nu sunt similare între ele se numește polinom (sau polinom). În acest caz, monomialele sunt termeni ai polinomului. Un polinom care conține două summands este numit binom (sau binomial).
Exemplu: p (x) = 3x2-5; h (x) = 5x-1
Un polinom care conține trei termeni se numește trinomial.
p (x) = un x n + an-1 x n-1 +. + a1 x 1 + a0
în cazul în care:
- an, an-1, an-2. a1, a0 sunt coeficienții polinomului. Ele pot fi numere naturale, întregi, raționale, reale sau complexe.
- an este coeficientul termenului cu cel mai mare exponent (coeficient de conducere)
- a0 este coeficientul termenului cu cel mai mic exponent (termen liber sau constant)
- n este gradul de polinom
p (x) = 5x3 -2x2 + 7x-1
- polinomul gradului III cu coeficienții 5, -2, 7 și -1
- 5 - raportul principal
- -1 - termen gratuit
- x este o variabilă
h (x) = - 2√3x4 + ½x-4
- polinomul gradului patru cu coeficienții -2√3, ½ și -4
- -2√3 - raportul de conducere
- -4 - membru gratuit
- x este o variabilă
Diviziunea de polinoame
Pentru a găsi coeficientul și restul împărțirii p (x) cu q (x). trebuie să utilizați următorul algoritm:- Gradul p (x) trebuie să fie mai mare sau egal cu gradul q (x).
- Trebuie să scriem ambele polinoame în ordinea descrescătoare a gradului. Dacă nu există nici un termen în p (x) cu orice putere, acesta trebuie completat cu un coeficient de 0.
- Termenul de conducere p (x) este divizibil de termenul de conducere q (x). iar rezultatul este scris sub linia de divizare (în numitor).
- Multiplicați rezultatul cu toți termenii q (x) și scrieți rezultatul cu semne opuse sub termenii p (x) cu puterile corespunzătoare.
- Adăugăm termeni cu termeni egali.
- Atribuiți termenii rămași p (x) la rezultat.
- Împărțiți termenul de conducere al polinomului obținut prin primul termen al polinomului q (x) și repetați pașii 3-6.
- Această procedură se repetă până când polinomul nou obținut are un grad mai mic decât q (x). Acest polinom va fi restul diviziunii.
- Polinomul, înregistrat sub linia de divizare, este rezultatul divizării (privată).
Exemplul 1
Pasul 1 și 2) $ p (x) = x ^ 5-3x ^ 4 + 2x ^ 3 + 7x ^ 2-3x + 5 \\ q (x) = x ^ 2-x +
3) x 5 -3x 4 + 2x 3 + 7x 2 -3x + 5
Răspuns: x 4 + 3x 2 + 2x - 8 = (x 2 - 3x) (x 2 + 3x + 12) + 38x - 8
Diviziunea pe un polinom de gradul I
Această diviziune poate fi efectuată utilizând algoritmul de mai sus, sau chiar mai rapid, dacă se folosește metoda lui Horner.
Dacă f (x) = an x n + an-1 x n-1 +. + a1 x + a0. polinomul poate fi rescris ca f (x) = a0 + x (a1 + x (a2 +. + x (an-1 + an x)))
q (x) este un polinom de gradul I → q (x) = mx + n
Atunci polinomul din coeficient va avea gradul n-1.
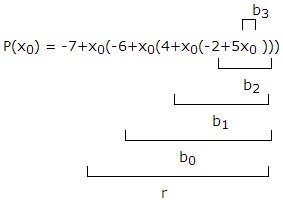
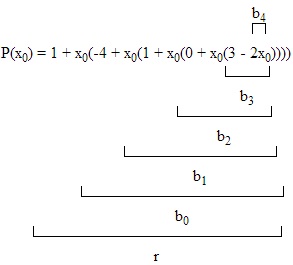
Exemplul 5
p (x) = 3x3 -5x2 + 2x + 3
q (x) = 2x-1
$ x_0 = \ frac $
p (x) = 3 + x (2 + x (-5 + 3x))
b2 = 3
$ b_1 = \ frac \ cdot 3-5 = - \ frac $
$ b_0 = \ frac \ cdot \ stânga (- \ frac \ dreapta) +2 = - \ frac + 2 = \ frac $
$ r = \ frac \ cdot \ frac + 3 = \ frac + 3 = \ frac \ Rightracrow c (x) = 3x ^ 2- \ fracx +
$ \ Rightarrow 3x ^ 3-5x ^ 2 + 2x + 3 = (2x1) (3x ^ 2 - \ fracx + \ frac) + \ frac $
concluzie
Dacă divizăm pe un polinom de grad mai mare decât unul, pentru a găsi coeficientul și restul, trebuie să folosim algoritmul 1-9.
Dacă divizăm pe polinomul primului grad mx + n. apoi pentru a găsi coeficientul și restul, trebuie să folosim metoda Horner cu $ x_0 = - \ frac $.
Dacă suntem interesați doar de restul diviziunii, este suficient să găsim p (x0).
Exemplul 6
p (x) = - 4x 4 + 3x 3 + 5x 2-x + 2
q (x) = x-1
x0 = 1
r = p (1) = - 4,1 + 3,1 + 5,1-1 + 2 = 5
r = 5
calculator
Articole similare
Trimiteți-le prietenilor: