În exemplele examinate mai devreme, probabilitățile evenimentelor elementare au fost calculate. Se pune întrebarea: cum să determinați probabilitatea unui eveniment dacă unele informații despre evenimente care au avut loc înainte de a fi cunoscute? [1] Probabilitatea evenimentului A. la calculul căruia sunt luate în considerare informațiile despre evenimentul B se numește condiționată și este notată ca P (A | B).
Probabilitatea evenimentului A, cu condiția ca evenimentul B să aibă loc, să fie egal cu probabilitatea evenimentului A și a evenimentului B. împărțit la probabilitatea evenimentului B:
Probabilitatea evenimentului B, cu condiția ca evenimentul A să aibă loc, să fie egal cu probabilitatea evenimentului A și B împărțit la probabilitatea evenimentului A:
unde P (A și B) sunt probabilitățile evenimentului A și B. P (A) este probabilitatea evenimentului A. P (B) este probabilitatea evenimentului B.
Descărcați nota în format Word sau PDF
De fapt, formulele (1) și (2) reprezintă o scurtă notație a probabilității condiționale bazate pe tabelul de caracteristici de urgență. Să revenim la exemplul considerat în nota anterioară (Figura 1). Să presupunem că știm că o familie va cumpăra un televizor cu ecran lat. Care este probabilitatea ca această familie să cumpere cu adevărat un astfel de televizor?

Fig. 1. Comportamentul cumpărătorilor de televizoare cu ecran lat
În acest caz, trebuie să calculați probabilitatea condiționată P (achiziția a fost efectuată, planificarea a fost planificată). Din moment ce știm că familia plănuiește o achiziție, spațiul eșantion nu constă din toate cele 1000 de familii, ci doar de cei care intenționează să achiziționeze un televizor cu ecran lat. Din cele 250 de astfel de familii, 200 au cumpărat de fapt acest televizor. Prin urmare, probabilitatea ca familia să cumpere de fapt un televizor cu ecran lat, dacă a planificat-o, poate fi calculată prin următoarea formulă:
P (achiziție se face | achiziție planificate) = numărul de familii care au planificat și au cumpărat un televizor / ecran lat număr de gospodării de planificare pentru a cumpăra un televizor cu ecran lat = 200/250 = 0,8
Acelasi rezultat este dat de formula (2):
unde evenimentul A este că familia plănuiește să cumpere un televizor cu ecran lat și evenimentul B - este că o va cumpăra cu adevărat. Înlocuind datele reale cu formula, obținem:
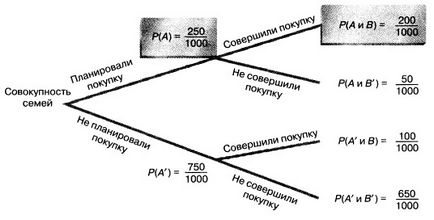
Fig. 2. Arborele de decizie
De exemplu, pentru a calcula probabilitatea ca o familie să cumpere un televizor cu ecran lat, dacă intenționează să facă acest lucru, ar trebui să determinați probabilitatea evenimentului în care achiziția este programată și terminată. și apoi împărțiți-o în probabilitatea unui eveniment de cumpărare programat. Deplasându-se de-a lungul pomului soluției prezentate în Fig. 2, obținem următoarele (similare cu cele anterioare):
În exemplul de a cumpăra un televizor cu ecran lat, probabilitatea ca o familie selectate aleatoriu achiziționat un televizor cu ecran lat, cu condiția ca ea a fost de planificare pentru a face acest lucru, este 200/250 = 0,8. Rețineți că probabilitatea necondiționată pe care o familie aleasă la întâmplare a achiziționat un televizor cu ecran lat este 300/1000 = 0,3. Aceasta duce la o concluzie foarte importantă. Informațiile a priori despre care familia intenționa să cumpere, afectează probabilitatea cumpărării în sine. Cu alte cuvinte, aceste două evenimente depind una de cealaltă. Spre deosebire de acest exemplu, există evenimente independente statistic, ale căror probabilități nu depind una de cealaltă. Independența statistică este exprimată prin identitatea: P (A | B) = P (A). unde P (A | B) - probabilitatea evenimentului A, cu condiția ca un eveniment sa produs B. P (A) - probabilitatea necondiționată a evenimentului A.
Observați că evenimentele A și B sunt independente din punct de vedere statistic unele de altele dacă și numai dacă P (A | B) = P (A). Dacă în tabela de situații de urgență a caracteristicilor având o dimensiune de 2 × 2, această condiție este îndeplinită pentru cel puțin o combinație de evenimente A și B. Aceasta va fi valabilă pentru orice altă combinație. În exemplul nostru, evenimentul de cumpărare este programat și achiziția este completă nu este independentă din punct de vedere statistic, deoarece informațiile despre un eveniment afectează probabilitatea celuilalt.
Să luăm în considerare un exemplu prin care să arătăm cum să verificăm independența statistică a două evenimente. Cerem 300 de familii care au cumpărat un televizor cu ecran lat, indiferent dacă sunt mulțumiți de achiziția lor (Figura 3). Determinați dacă gradul de satisfacție cu achiziția și tipul de televizor sunt corelate unul cu celălalt.
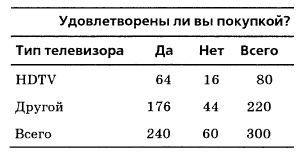
Fig. 3. Datele care caracterizează gradul de satisfacție a clienților cu televizoarele cu ecran lat
Judecând după aceste date,
P (cumpărătorul este mulțumit) = 240/300 = 0.80
Prin urmare, probabilitatea ca cumpărătorul este mulțumit de cumpărare, și că familia a cumpărat HDTV-TV, egale între ele, iar aceste evenimente sunt independente statistic, pentru că în nici un fel legate.
Regula pentru multiplicarea probabilităților
Formula pentru calculul probabilității condiționale ne permite să determinăm probabilitatea unui eveniment comun A și B. Având formula rezolvată (1)
relativ la probabilitatea comună P (A și B). obținem o regulă generală pentru multiplicarea probabilităților. Probabilitatea evenimentului A și B este egală cu probabilitatea evenimentului A, cu condiția să se fi produs un eveniment B înmulțit cu probabilitatea evenimentului B:
(3) P (A și B) = P (A | B) * P (B)
Luați în considerare, ca exemplu, 80 de familii care au cumpărat un HDTV-TV cu ecran lat (Figura 3). Tabelul indică faptul că 64 de familii sunt mulțumite de cumpărare și 16 nu sunt. Să presupunem că două familii sunt alese aleator printre ei. Determinați probabilitatea ca ambii cumpărători să fie satisfăcuți. Folosind formula (3), obținem:
P (A și B) = P (A | B) * P (B)
în cazul în care evenimentul A este faptul că a doua familie este mulțumită de cumpărarea lor, iar evenimentul B este acela că prima familie este mulțumită de cumpărarea lor. Probabilitatea ca prima familie să fie mulțumită de achiziția lor este de 64/80. Cu toate acestea, probabilitatea ca a doua familie să fie de asemenea mulțumită de cumpărarea lor, depinde de răspunsul primei familii. În cazul în care prima familie după votare nu returnează proba (eșantionare fără înlocuire), numărul de respondenți este redus la 79. Când a fost prima familie mulțumit cu achiziția dvs., probabilitatea ca cealaltă familie, de asemenea, va fi fericit, este 63/79, pentru că numai 63 au rămas în eșantion familiilor mulțumiți de achiziția lor. Astfel, substituind date specifice în formula (3), primim următorul răspuns:
P (A și B) = (63/79) (64/80) = 0,638.
În consecință, probabilitatea ca ambele familii să fie mulțumite de achizițiile lor este de 63,8%.
Să presupunem că după anchetă prima familie revine la eșantion. Determinați probabilitatea ca ambele familii să fie mulțumite de cumpărarea lor. În acest caz, probabilitatea ca ambele familii să fie mulțumite de achiziția lor sunt aceleași și egale cu 64/80. În consecință, P (A și B) = (64/80) (64/80) = 0,64. Astfel, probabilitatea ca ambele familii să fie mulțumite de achizițiile lor este de 64,0%. Acest exemplu arată că alegerea celei de-a doua familii nu depinde de alegerea primei familii. Astfel, înlocuind în (3) probabilitatea condiționată P (A | B) cu probabilitatea P (A). obținem formula pentru multiplicarea probabilităților evenimentelor independente.
Regula pentru multiplicarea probabilităților evenimentelor independente. Dacă evenimentele A și B sunt independente din punct de vedere statistic, probabilitatea evenimentului A și B este probabilitatea evenimentului A. înmulțit cu probabilitatea evenimentului B.
Dacă această regulă este îndeplinită pentru evenimentele A și B. atunci ele sunt independente din punct de vedere statistic. Astfel, există două modalități de determinare a independenței statistice a două evenimente:
- Evenimentele A și B sunt independente din punct de vedere statistic unele de altele dacă și numai dacă P (A | B) = P (A).
- Evenimentele A și B sunt independente din punct de vedere statistic unele de altele dacă și numai dacă P (A și B) = P (A) P (B).
Dacă în tabelul de situații de urgență cu caracteristici având dimensiunea de 2 × 2, una dintre aceste condiții este îndeplinită pentru cel puțin o combinație de evenimente A și B. Aceasta va fi valabilă pentru orice altă combinație.
Probabilitatea necondiționată a unui eveniment elementar
unde evenimentele B1. B2. ... Bk sunt reciproc exclusive și exhaustive.
Să ilustrăm aplicarea acestei formule în exemplul din Fig. Folosind formula (5), obținem:
unde P (A) este probabilitatea ca achizitia a fost planificata, P (B1) este probabilitatea ca achizitia sa fie finalizata, P (B2) este probabilitatea ca achizitia sa nu fie finalizata.
Probabilitatea condiționată a unui eveniment ia în considerare informațiile pe care a avut loc un alt eveniment. Această abordare poate fi folosită atât pentru a rafina probabilitatea luând în considerare informațiile nou-venite, cât și pentru a calcula probabilitatea ca efectul observat să fie o consecință a unei cauze specifice. Procedura de rafinare a acestor probabilități se numește teorema lui Bayes. A fost inițial dezvoltată de Thomas Bayes în secolul al XVIII-lea.
Să presupunem că societatea menționată mai sus examinează piața pentru vânzarea unui nou model TV. În trecut, 40% dintre televizoarele create de companie au avut succes, iar 60% dintre modele nu au primit recunoaștere. Înainte de a anunța lansarea unui nou model, comercianții examinează cu atenție piața și fixează cererea. În trecut, succesul a 80% dintre modelele care au primit recunoaștere a fost anticipat în avans, în timp ce 30% dintre previziunile favorabile s-au dovedit a fi greșite. Pentru noul model, departamentul de marketing a dat o perspectivă favorabilă. Care este probabilitatea ca noul model TV să fie în căutare?
Teorema lui Bayes poate fi derivată din definițiile probabilității condiționale (1) și (2). Pentru a calcula probabilitatea P (B \ A), luăm formula (2):
și substituie pentru P (A și B) valoarea de la formula (3):
P (A și B) = P (A | B) * P (B)
Substituind formula (5) pentru P (A), obținem teorema lui Bayes:
unde evenimentele B1. B2. ... Bk sunt reciproc exclusive și exhaustive.
Să prezentăm următoarea notație: evenimentul S-TV este solicitat. evenimentul S '- televizorul nu este în căutare. eveniment F - prognoză favorabilă. evenimentul F 'este o prognoză nefavorabilă. Să presupunem că P (S) = 0.4, P (S ') = 0.6, P (F | S) = 0.8, P (F | S') = 0.3. Aplicând teorema Bayes obținem:
Probabilitatea cererii pentru un nou model TV, sub rezerva unei previziuni favorabile, este de 0,64. Astfel, probabilitatea unei lipsuri a cererii în condițiile unei prognoze favorabile este de 1-0,64 = 0,36. Procesul de calcul este prezentat în Fig. 4.

Fig. 4. (a) Calculul folosind formula Bayes pentru estimarea probabilității cererii pentru televizoare; (b) Arborele de decizie atunci când investighează cererea pentru un nou model TV
Să luăm în considerare un exemplu de aplicare a teoriei Bayes pentru diagnosticarea medicală. Probabilitatea că o persoană suferă de o anumită boală este de 0,03. Un test medical vă permite să verificați dacă este așa. Dacă o persoană este într-adevăr bolnavă, probabilitatea unui diagnostic corect (afirmând că o persoană este bolnavă când este într-adevăr bolnavă) este de 0,9. Dacă o persoană este sănătoasă, probabilitatea unui diagnostic fals pozitiv (care afirmă că o persoană este bolnavă atunci când este sănătoasă) este de 0,02. Să presupunem că un test medical a dat rezultate pozitive. Care este probabilitatea că o persoană este într-adevăr bolnavă? Care este probabilitatea unui diagnostic precis?
Introducem următoarea notație: evenimentul D - persoana este bolnavă. evenimentul D - persoana este sănătoasă. eveniment T - diagnosticul este pozitiv. evenimentul T '- diagnosticul este negativ. Rezultă din starea problemei că P (D) = 0,03, P (D ') = 0,97, P (T | D) = 0,90, P (T | D') = 0,02. Aplicând formula (6), obținem:
Probabilitatea că o persoană este într-adevăr bolnavă cu un diagnostic pozitiv este de 0,582 (a se vedea și Figura 5). Rețineți că numitorul formulei Bayes este egal cu probabilitatea unui diagnostic pozitiv, adică 0.0464.
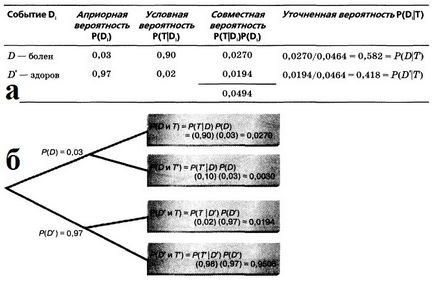
Fig. 5. (a) calcule bayesiene pentru a estima corectitudinea diagnosticului medical; (b) arborele de decizie pentru evaluarea corectitudinii diagnosticului medical
Ați putea fi, de asemenea, interesat de:
Articole similare
Trimiteți-le prietenilor: