Opr1. Un vector se numește o bază pe linia L dacă vectorul || L poate fi scris în formă
Două vectori independenți liniari situați în planul P sunt numiți baza pe planul P dacă vectorul aflat pe planul P poate fi scris în formă.
3. Trei vectori independenți liniar sunt numiți o bază în spațiu dacă vectorul poate fi scris în formă
1. Orice vector non-zero formează o bază pe linia L.
2. Orice pereche de vectori necoliniari situați în planul P formează o bază pe planul P
3. Orice triple de vectori necoplanari formează o bază în spațiu.
(2) în plan
(3) în spațiu
Opp4 Partea dreaptă a formulelor (1), (2), (3) se numește extinderea vectorilor pe bază; ; respectiv, numărul de coordonate corespunzătoare.
Teorema 1: Extinderea bazei este unică (independent!)
Teorema 2: Când se adaugă vectorii, se adaugă coordonatele respective. Atunci când vectorul este înmulțit cu numărul, coordonatele sale se înmulțesc cu acest număr
18. Proiecția vectorului pe axă. Sistemul de coordonate carteziene. Conductoare cosinale.
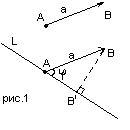
Op1: Un vector se numește proiecția vectorială a vectorului pe axa L.
Opp2: Proiecția scalară a vectorului pe axa L este:
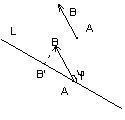
Fixați asta. Să considerăm triplu i, j, k (i ^ j) = (i ^ k) = (j ^ k) =; | i | = | j | = | k | = 1 ;. punct O - punctul de plecare general. Vectorul i definește axa Ox, j este axa Oy și k este axa Oz.
Astfel, am introdus coordonatele carteziene în spațiu. Fie m un punct arbitrar. Completăm paralelipipedul dreptunghiular cu diagonala OM.
Lungimile marginilor | x |, | y |, | z |. Coordonatele TM sunt numere reale x, y, z;
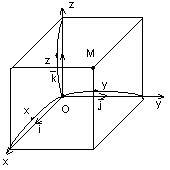
Declarație: coordonatele carteziane ale punctelor coincid cu proiecțiile scalare ale vectorului pe axele corespunzătoare:
- dreptunghiular; y = OA = | | cos = | | cos =
În mod similar pentru x și z.
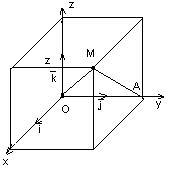
Op: Cantitățile ,, sunt denumite direcțiile cosinilor ale vectorului.
Împărțim ambele părți ale ecuației
19. Produs scalar al vectorilor și proprietățile acestora.
Opredelnie: Valoarea (a, b) = | A | * | b | * cos (a ^ b) se numește bulevardul interior mânca vectori a și b. Evident, putem scrie (a, b) = | A | * (proiecție b pe o) și vice-versa.
Proprietățile unui produs scalar:
4) (a, a) ≥0, unde (a, a) = 0 când a = 0.
(proiecția b pe a) + | a | * (proiecția lui c pe a) = (a, b) + (a, c) produsul .Skalyarnoe este egal cu 0 dacă și numai dacă b perpendicular sau a = 0 sau b = 0.
20. Produsul vectorial al vectorilor și proprietățile acestora. Condiții necesare și suficiente pentru colinearitatea vectorilor.
Opredelnie: Vectorul c se numește produsul vectorial al unui și b, notată cu c = [a, b], dacă | c | = | A | * | b | * sin (a ^ b), c perpendicular pe a și b, dreapta ABC- triplu.
Proprietățile produsului vectorial:
Lemma a = b ó pentru orice d (a, d) = (b, d)
- sfârșitul lucrului -
Acest subiect aparține secțiunii:
Matricea A a dimensiunii Sxn este o masă dreptunghiulară formată din rânduri S și coloane n. elementul matrice.
Ce vom face cu materialul:
Trimiteți-le prietenilor: