Funcțiile a două variabile: \ (f \ left (\ right) \), \ (g \ left (\ right) \)
Variabilele independente sunt: \ (x \), \ (y \), \ (u \), \ (v \)
Creșteri mici: \ (\ Delta \), \ (\ Delta \)
Domeniile de integrare sunt: \ (R \), \ (S \)
Numerele reale sunt: \ (a \), \ (b \), \ (c \), \ (d \), \ (\ alpha \), \ (\
Polar coordonate: \ (r \), \ (\ theta \)
Domeniul domeniului: \ (A \)
Aria suprafeței: \ (S \)
Volumul corpului: \ (V \)
Masa plăcii: \ (m \)
Densitatea plăcii: \ (\ rho \ left (\ right) \)
Primele momente: \ (\), \ (\)
Momente de inerție: \ (\), \ (\), \ (\)
Plăcuța plăcii: \ (Q \)
Densitatea încărcării: \ (\ sigma \ left (\ right) \)
Coordonatele centrului de masă sunt: \ (\ bar x \), \ (\ bar \ \)
Valoarea medie a funcției: \ (\ mu \)
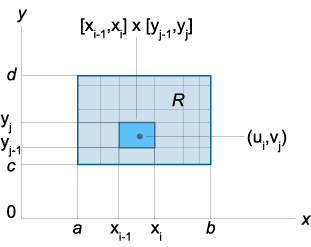
Integrul dublu al funcției \ (\ left \ (right) \) în regiunea dreptunghiulară \ (\ left \ \ right \ \ times \ left \ \ right) \ este definit ca limita sumelor integrale (suma Riemann)
\ (\ Solicite \ mare \ iint \ limits_ \ dreapta] \ ori \ stânga [\ dreapta]> \ normalsize \ dreapta) dA> = \ lim \ limite _ \, \ Delta \ la 0 \\ \ textul \, \ Delta \ la 0 >> \ suma \ limits_ ^ m ^ n,> \ dreapta) \ Delta \ Delta >>, \)
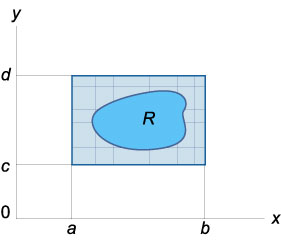
Dubla integrală a funcției \ (f \ stânga (\ dreapta) \) într-un domeniu \ arbitrar (R \) este determinată ca \ (\ mare \ iint \ limits_R \ normalsize \ dreapta) dA> = \ mare \ iint \ limits_ \ right] \ times \ left [\ right]> \ normaliza \ dreapta] dA>, \)
dreptunghiul \ (\ stânga [\ dreapta] \ ori \ stânga [\ dreapta] \) cuprinde o regiune de \ (R \), funcția \ (g \ left (\ dreapta) = f \ left (\ dreapta) \), dacă \ (f \ left (\ right) \) se află în \ (R \) și \ (g \ left (\ right) = 0 \) altfel.
Integrul dublu al sumei funcțiilor este egal cu suma integralelor acestor funcții:
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) + g \ left (\ dreapta)> \ right] dA> = \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> + \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> \)
Integrul dublu al diferenței de funcții este egal cu diferența dintre integralele acestor funcții:
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) - g \ stânga (\ dreapta)> \ right] dA> = \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> - \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> \)
Coeficientul constant poate fi considerat ca semn integrat dublu:
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) dA> = k \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> \)
Dacă \ (f \ left (\ right) \ le g \ left (\ right) \) în domeniul \ (R \), atunci inegalitatea
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) dA> \ le \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> \)
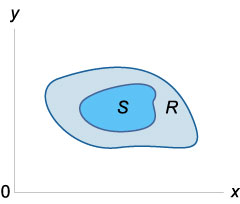
Dacă \ (f \ left (\ right) \ ge 0 \) în domeniul \ (R \) și \ (S \ subsetul R \), atunci
\ (\ Mare \ iint \ limits_S \ normalsize \ dreapta) dA> \ le \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> \)
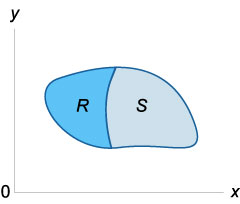
Dacă \ (f \ stânga (\ dreapta) \ ge 0 \) în \ (R \) și \ (R \) și \ (S \) - zona care nu se suprapun,
\ (\ Mare \ iint \ limits_ \ normalsize \ dreapta) dA> = \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> + \ mare \ iint \ limits_S \ normalsize \ dreapta) dA> \)
Aici \ (\) este uniunea regiunilor de integrare a \ (R \) și \ (S \).
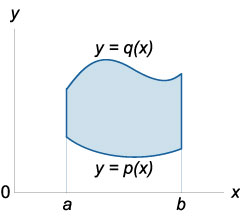
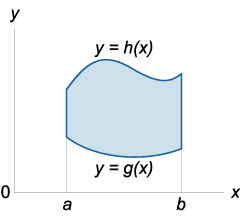
unde domeniul de integrare \ (R \) este determinat de inegalități
\ (R = \ left \<\left( \right) \mid a \le x \le b,\;p \left( x \right) \le y \le q\left( x \right)\right\>\).
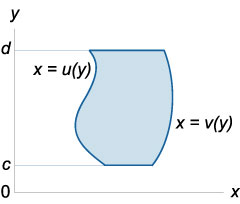
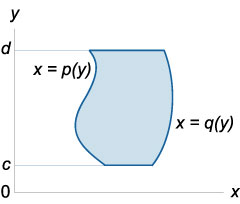
unde domeniul de integrare \ (R \) este determinat de inegalități
\ (R = \ left \<\left( \right) \mid u\left( y \right) \le x \le v\left( y \right),\;c \le y \le d \right\>\).
Complet dublu într-o regiune dreptunghiulară
Dacă \ (R \) este o regiune dreptunghiulară \ (\ left [\ right] \ times \ left [\ right] \), atunci
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) dA> = \ mare \ int \ limits_a ^ b \ normalsize \ dreapta) dy >> \ dreapta) dx> = \ mare \ int \ limits_c ^ d \ normalsize \ dreapta ) dx >> \ dreapta) dy> \)
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) dxdy> = \ mare \ iint \ limits_R \ normalsize = \ stânga (> \ dreapta) \ stânga (> \ dreapta) \)
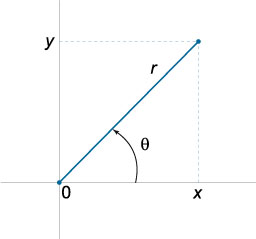
Polar coordonate
\ (x = r \ cos \ theta, y = r \ sin \ theta \)
Integral dublu în coordonate polare
Diferența \ (dxdy \) în coordonate polare este dată de
\ (dxdy = \ left | \ right) >> \ right) >> \ normalsize> \ dreapta | drd \ theta = rdrd \ theta \)
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) dxdy> = \ mare \ int \ limits_ \ alpha ^ \ beta \ normalsize ^ \ normalsize \ dreapta) rdrd \ theta >> \)
Integral dublu în dreptunghiul polar
Dacă regiunea de integrare \ (R \) este un dreptunghi polar. (\ beta \ \ alpha \ le \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ integrarea este
\ (\ Mare \ iint \ limits_R \ normalsize \ dreapta) dxdy> = \ mare \ int \ limits_ \ alpha ^ \ beta \ normalsize \ dreapta) rdrd \ theta >> \)
Volumul corpului
\ (V = \ large \ iint \ limits_R \ normaliza \ dreapta) dA> \)
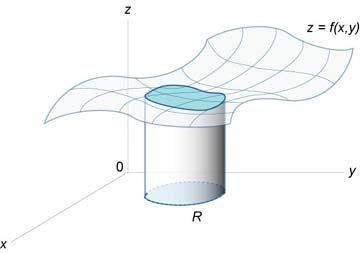
\ (V = \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> = \ mare \ int \ limits_a ^ b \ normalsize ^ \ normalsize \ dreapta) dydx >> \) Dacă \ (R \) este un tip de suprafață \ (II \) și delimitată de liniile \ (y = c \), \ (y = d \), \ (x = q \ stânga (y \ dreapta) \), \ ( x = p \ left (y \ right) \), apoi
\ (V = \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> = \ mare \ int \ limits_c ^ d \ normalsize ^ \ normalsize \ dreapta) dxdy >> \)
Volumul corpului între două suprafețe
Dacă \ (\ left \ (\ right) \ ge g \ left (\ right) \) în regiunea \ (R \), atunci volumul corpului dintre suprafețele \ \ right) \) în această zonă este egal cu
\ G \ stânga (\ dreapta)> \ dreapta] dA> \)
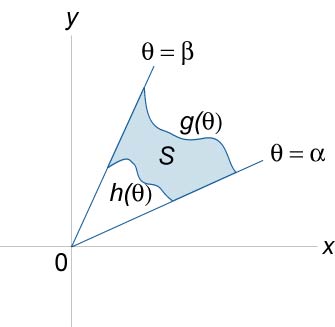
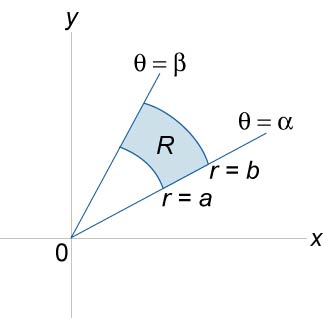
Să presupunem că domeniu \ (S \) este definit în coordonate polare în planul \ (Oxy \) și delimitate prin linii \ (\ theta = \ alpha \), \ (\ theta = \ beta \) \ (r = h \ left (\ theta \ right) \), \ (r = g \ stânga (\ theta \ right) \). Să presupunem de asemenea că o funcție \ (f \ left (\ right) \) este dată în domeniul \ (S \). Apoi, domeniul domeniului \ (S \) și volumul corpului delimitat de suprafață \ (f \ left (\ right) \) sunt definite prin formule
\ (A = \ mare \ iint \ limits_S \ normalsize = \ mare \ int \ limits_ \ alpha ^ \ beta \ normalsize ^ \ normalsize> \; \; V = \ mare \ iint \ limits_S \ normalsize \ dreapta) rdrd \ theta> \)

Greutatea plăcii
\ (m = \ mari \ iint \ limits_R \ normalsize \ dreapta) dA> \)
Plăcuța este situată în regiunea \ (R \) și densitatea acesteia la punctul \ (\ right)> \) este egală cu \ (\ right)> \).
Momente statice ale plăcii
Momentul plăcii în raport cu axa | (Ox |) este dat de
\ (\ \ mari \ iint \ limits_R \ normalsize \ dreapta) dA> \)
În mod similar, momentul plăcii în raport cu axa \ (Oy \) este exprimat ca
\ (\ \ mari \ iint \ limits_R \ normalsize \ dreapta) dA> \)
Momente de inerție ale plăcii
Momentul inerției plăcii în raport cu axa \ (Ox \) se calculează de la
\ (\ mare \ iint \ limits_R \ normalsize \ rho \ stânga (\ dreapta) dA> \)
Momentul inerției plăcii în raport cu axa \ (Oy \) este egal cu
\ (\ mare \ iint \ limits_R \ normalsize \ rho \ stânga (\ dreapta) dA> \)
Momentul polar al inerției este dat de
\\ \\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\ "
Placă de încărcare
\ (Q = \ mare \ iint \ limits_R \ normalsize \ dreapta) dA> \),
unde încărcătura electrică este distribuită în regiunea \ (R \) și densitatea acesteia la punctul \ (\ right)> \) este egală cu \ (\ right)> \).
Media funcției
\ (\ Mu = \ mare \ frac \ iint \ limits_R \ normalsize \ dreapta) dA> \; \) unde \ (S = \ mare \ iint \ limits_R \ normalsize \).
Articole similare
Trimiteți-le prietenilor: