Metoda de factorizare a matricei
Una dintre metodele cele mai eficiente de restabilire a formei 3D și a mișcării unui obiect este metoda bazată pe factorizarea matricelor. Să explicăm esența metodei pentru aproximări lineare. Sa arătat mai sus că ecuațiile care descriu aproximări lineare au forma (2.3.20):
Formăm din coordonate o matrice de măsurare W de dimensiune 2F x P:

Fiecare rând al matricei W conține coordonatele punctelor (ufp, vfp) aferente cadrului specific al secvenței și fiecare coloană - aceleași valori pentru punctul particular prezent în toate imaginile. Apoi expresia (2.3.33) poate fi rescrisă în forma matriceală:
unde M - mișcare matrice (orientarea aparatului foto) de dimensiune 2F x 3, S - formă de matrice (punctul de pe obiect), marimea 3 x P, T - emisiuni vectoriale camere (poziții ale camerei în spațiu), dimensiunile 2F x 1, format după cum urmează:

Plasăm începutul MSC în CM a punctelor obiectului (2.3.10):
Observăm că vectorul T poate fi obținut printr-o sumare a rândului elementelor matricei W:
atunci vom continua să lucrăm cu matricea W *:
Deoarece matricea W * este produsul dimensiunea matricei M și 2F x 3 matrice S 3 x P dimensiunea, rangul său nu poate fi mai mare decât 3. În această implementare a matricei factorizării rangul 3 W, produs prin descompunerea matricei singular (SVD):
Aici U, V - matricele ortogonale și U = diag (y1, ..., yn), n = min (2F, P), y1, ..., yn - valori singulare ale ordinului W. matrice toate valorile singulare, în ordine descrescătoare, și selectați din la submatricea superioară a dimensiunii matricei 3 x 3 ale căror valori sunt număr singular maxim 3 corespunzând principalelor componente ale matricei W. Apoi, alegând din matrici U și V din rândurile submatricea corespunzătoare celei mai mari trei valoare singulară, obținem o aproximare a matricei W. se înțelege că o astfel de expansiune nu este unică, deoarece Mezhuyev matrici M) și S) este întotdeauna posibil să se introducă pro Instituția matricei directă și inversă de rangul 3 Q, nimic nu se schimbă, atunci putem scrie:
Aici M și S implică matrici adevărate de mișcare și formă.
obținem următoarele sisteme de ecuații pentru aproximări pentru găsirea matricei Q:
În cazul în care valorile corespund tabelului 2.3.2. (a se vedea și tabelul 2.3.1)

În această lucrare, sistemele (2.3.41) au fost rezolvate prin metoda celor mai mici pătrate (OLS) folosind SVD.
etapa de recuperare a formei Ambiguitate datorită faptului că sarcina poate face cu ușurință ambiguitate simbolică, înlocuind matricea Q cu următoarea matrice:
Fixarea orientării axelor sistemului de coordonate, de exemplu, alegerea direcției axelor este aceeași ca și pentru un sistem conectat la unul dintre camere, ambiguitatea din primele două caractere poate fi eliminată. Luând în considerare alinierea față de prima cameră, obținem matricele de mișcare și formă necesare:
Ambiguitatea în cel de-al treilea semn se datorează faptului că, în toate aproximările lineare considerate de noi, adâncimea obiectului este neglijată în comparație cu distanța față de acesta (are loc așa-numita "aplatizare" a scenei). În consecință, aceasta conduce la ambiguitatea reconstrucției formei scenei S și a mișcării camerelor M.
Metoda iterativă pentru rezolvarea problemelor 3D
Principalele dezavantaje ale aproximarea liniară menționată mai sus este ambiguitatea în determinarea semnului adâncimea scenei și incapacitatea de a calcula lungimi focale ale camerelor de luat vederi. Prezența în imagini a denaturărilor de perspectivă reprezintă o sursă suplimentară de informații care ajută la eliminarea deficiențelor enumerate.
Deoarece metoda este corectă, este descrisă uravneiyami (03/02/39), în care am pus g constantă pentru toate cadrele.
Vom rescrie (2.3.44) în formular, folosind substituția zf deja întâlnită:
Astfel, partea dreapta a ecuațiilor obținute corespunde partea dreaptă a ecuațiile pentru MOSFET (2.3.17), iar partea stanga este suma partea stângă a aproximări liniare și aditivi. În forma matricei, obținem acum:

Ie matricea W este reprezentată ca doi termeni, primul dintre ei, W1, corespunde matricei de măsurare introduse anterior, iar cea de-a doua, W2, depinde de W1, sp, kf și are sens să corecteze distorsiunile de perspectivă:
După cum sa arătat anterior, gradul de pe partea dreapta (2.3.45) este întotdeauna egal cu 3, se propune să selecteze iterații ale parametrului b folosind cunoscute din sp valoarea etapa anterioară, KF, astfel încât să se păstreze egalitatea rândurile ambelor părți (02/03/45). Astfel, sistemul de ecuații (2.3.45) pot fi rezolvate iterativ, prin clarificarea matricei de corecție.
Algoritmul iterativ propus funcționează bine în cazul unei orientări centrale pe obiect, datorită faptului că într-o aproximare inițială MOS ales - proiecție. Dacă există o necesitate esențială de a lucra strict în situația orientării non-centrale, este mai adecvat să o folosiți ca un îndrumător
din aproximarea inițială este o proiecție parappectivă. Să formulăm algoritmul propus pentru rezolvarea problemei de recuperare neliniară.
1. Presupunem în (2.3.46) Number iterație q = 0, parametrul S = 0, W (0): = W1, W2 (0): = 0.
2. Rezolvăm sistemul de ecuații care descrie aproximarea MOS:
3. Acum setăm: q: = q + 1.
4. Calculați matricea de corecție:
5. Vom găsi coeficientul b (q), alegându-l ca gradul de W matrice (q) rămâne egal cu 3, care urmează să fie căutat:
unde y1, y4 reprezintă prima și a patra valoare singulară a matricei W (q). Intervalul variației parametrului 6 (q) este determinat din starea:
6. Actualizăm matricea
7. Mergeți la pasul 2 dacă condiția de ieșire nu este îndeplinită:
unde valoarea e este aleasă suficient de mică.
8. Eliminăm ambiguitatea semnului profunzimii scenei:
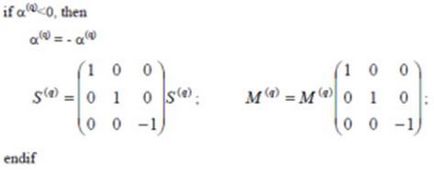
9. Aliniați MSC cu CC asociat cu una din camere.
Articole similare
Trimiteți-le prietenilor: