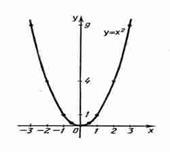
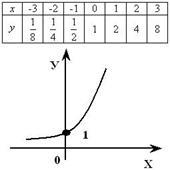
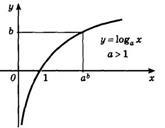
4. Graficul funcției logaritmice trece întotdeauna prin punctul (1; 0).
5. Funcția logaritmică crescătoare va fi pozitivă pentru x> 1 și negativă pentru 0<х<1.
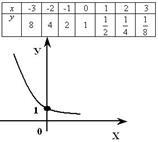
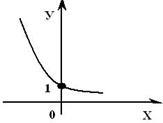
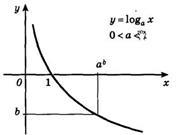
Figura următoare prezintă un grafic al funcției logaritmice descrescătoare - (0
7. Funcția nu este uniformă sau ciudată. Funcția logaritmică este o funcție a formei generale.
8. Funcția nu are puncte maxime și minime.
Domeniul funcției este setul tuturor numerelor reale. Setul de valori ale funcției este intervalul [-1; 1], adică funcția sinusoidală este limitată. Funcția este impare: sin (-x) = - sin x pentru toate x ∈ R. Graficul grafic al funcției este simetric în raport cu originea. Funcția periodică cu cea mai mică perioadă pozitivă 2π. sin (x + 2π · k) = sin x, unde k ∈ Z pentru toate x ∈ R. sin x = 0 pentru x = π · k. k ∈ Z. sin x> 0 (pozitiv) pentru toate x ∈ (2π · k · π + 2π · k), k ∈ Z. sin x <0 (отрицательная) для всех x ∈ (π+2π·k. 2π+2π·k ), k ∈ Z.
Funcția crește de la -1 la 1 la intervale:
Funcția scade de la -1 la 1 la intervale:
- La x 0 - graficul rămâne neschimbat,
- la x <0 — график симметрично отражается относительно оси ординат.
21)) Setul de numere, fiecare dintre ele având propriul număr n (n = 1, 2, 3), se numește o secvență numerică.
Numerele individuale ale unei secvențe sunt numite membrii ei și sunt de obicei denumiți de primul termen a1. al doilea a2. al n-lea termen etc. Ansamblul secvenței numerice este notat cu
22) Progresia aritmetică. O secvență numerică, fiecare membru din care, începând cu a doua, este egală cu cea precedentă, pliată cu un număr constant d pentru această secvență, se numește o progresie aritmetică. Numărul d este numit diferența progresiei. Orice membru al progresiei aritmetice este calculat de formula:
Suma primelor n termeni ai progresiei aritmetice se calculează astfel:
Progresia geometrică. O secvență numerică, fiecare membru din care, începând cu al doilea, este egală cu cea precedentă, înmulțită cu un număr constant q pentru această secvență. se numește geometric
progresia bolii. Numărul q este numit numitorul progresiei. Orice membru al unei progresii geometrice este calculat de formula:
Suma primilor termeni n ale progresiei geometrice se calculează astfel:
O progresie geometrică infinită se numește o progresie geometrică infinit descendentă, numitorul căruia satisface condiția.
Cu o creștere neîngrădită, suma primelor termeni dintr-o evoluție geometrică descendentă infinită tinde către un număr. care se numeste suma unei progresii geometrice infinit de descreștere.
) Derivatul funcției f (x), f '(x). ea însăși este o funcție. În acest fel, derivatul funcției f (x) este numit derivatul ordinii a doua (sau cel de-al doilea derivat).
Semnificația geometrică a derivatului. Derivatul la punctul x 0 este egal cu panta tangentei la graficul funcției y = f (x) în acest punct.
Ecuația tangentei la graficul funcției: y = f (a) + f '(a) (x - a) y = f (a) + f'
Sensul fizic al derivatului. Dacă punctul se deplasează de-a lungul axei x și coordonatele sale se modifică în conformitate cu legea x (t), atunci viteza instantanee a punctului:
24)) Derivarea sumei (diferenței) funcțiilor
Derivatul sumelor algebrice ale funcțiilor este exprimat de următoarea teoremă.
Derivatul sumei (diferenței) dintre două funcții diferențiate este egal cu suma (diferența) derivatelor acestor funcții:
Derivatul unei sume algebrice finite de funcții diferențiate este egal cu aceeași sumă algebrică a derivatelor sumelor. De exemplu,
Articole similare
Trimiteți-le prietenilor: