Folosind ecuațiile diferențiale de mișcare, se rezolvă a doua problemă a dinamicii. Regulile pentru compunerea unor astfel de ecuații depind de modul în care vrem să determinăm mișcarea unui punct.
1) Determinarea mișcării unui punct printr-o metodă de coordonate.
Luați în considerare un punct material liber care se mișcă sub acțiunea forțelor. Desenăm axele fixe de coordonate Oxyz (figura 4). Proiectând ambele părți ale egalității pe aceste axe și ținând seama de acestea etc. obținem ecuațiile diferențiale ale mișcării curbilinii ale punctului în proeminențele de pe axa sistemului de coordonate carteziene dreptunghiulare:
Deoarece forța care acționează asupra unui punct poate depinde de timpul și poziția punctului vitezei sale, atunci laturile din dreapta ale ecuațiilor pot conține timpul t, coordonatele punctului x, y, z și proiecția vitezei sale. Partea dreaptă a fiecărei ecuații poate include toate aceste variabile.
Pentru a rezolva problema de bază dinamică cu ajutorul acestor ecuații, este necesar ca, pe lângă forțele care acționează, să cunoască și condițiile inițiale, adică poziția și viteza punctului la momentul inițial. În axele de coordonate Oxyz, condițiile inițiale sunt date în forma:
Cunoscând forțele care acționează, după integrarea ecuațiilor, găsim coordonatele x, y, z ale punctului mobil în funcție de timpul t, adică găsim legea de mișcare a punctului.
Exemplu corp de mișcare 3. Studiul aruncat cu viteza inițială, la un unghi față de orizontală, considerând ca material m punct de masă. Aceasta neglijează rezistența aerului și câmpul gravitațional își va asuma uniform (F = const), presupunând că distanța de zbor și înălțimea traiectoriei Mic în comparație cu raza Pământului.
Am plasat originea O în poziția inițială a punctului. Direcționați axa vertical în sus; Aranjăm axa orizontală Ox în planul care trece prin Oy și vectorul. iar axa Oz este perpendiculară pe primele două axe (figura 5). Apoi, unghiul dintre vector și axa Ox este egal cu.
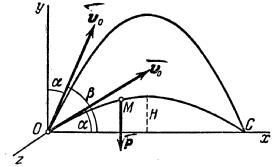
Să reprezentăm punctul de mișcare M undeva pe traiectorie. Doar forța gravitațională acționează asupra punctului. ale căror proiecții pe axa de coordonate sunt :. . .
Înlocuind aceste cantitati in ecuatii diferentiale si notand ca, etc. vom obține după reducerea cu m:
Înmulțind ambele părți ale acestor ecuații prin dt și integrând, găsim:
Condițiile inițiale în problema noastră au forma:
Respectând condițiile inițiale, vom avea:
Înlocuind aceste valori ale lui C1. C2 și C3 în soluția găsită mai sus și înlocuind. la venirea la ecuații:
Integrarea acestor ecuații, obținem:
Înlocuirea datelor inițiale dă C4 = C5 = C6 = 0, iar în cele din urmă găsim ecuațiile de mișcare pentru punctul M în forma:
Rezultă din ultima ecuație că mișcarea are loc în planul Oxy.
Având ecuația de mișcare a unui punct, este posibil să determinăm prin metodele cinematice toate caracteristicile unei mișcări date.
1. Traiectoria unui punct. Eliminând timpul t din primele două ecuații (1), obținem ecuația traiectoriei punctului:
Aceasta este ecuația parabolică cu o axă paralelă cu axa Oy. Astfel, un punct greu, aruncat sub un unghi la orizont, se mișcă într-un spațiu fără aer, de-a lungul unei parabole (Galileo).
2. Interval orizontal. Definiți intervalul orizontal, adică Distanța OC = X măsurată de-a lungul axei OX. Presupunând că y = 0 în (2), găsim punctele de intersecție a traiectoriei cu axa Ox. Din ecuația:
Prima soluție dă punctul O la al doilea punct C. În consecință, X = X2 și în final
Se poate observa din formula (3) că același interval orizontal X va fi obținut sub un unghi. pentru care. și anume dacă este un unghi atât de mare. Prin urmare, pentru o viteză inițială dată, pot fi atinse două traiectorii în același punct C: on-stylish () și articulat ().
La o anumită viteză inițială, intervalul orizontal maxim într-un spațiu fără aer este obținut când. și anume la un unghi.
3. Înălțimea traiectoriei. Dacă punem în ecuație (2)
. atunci există o altitudine a traiectoriei H:
4. Timpul zborului. Din prima ecuație a sistemului (1) rezultă că timpul total de zbor T este determinat de egalitate. Înlocuindu-l pe X cu valoarea sa, obținem
La unghiul celui mai lung interval, toate cantitățile găsite sunt egale:
Rezultatele sunt practic complet aplicabile pentru orientabile-cochilii tirovochnogo determinarea caracteristicilor de zbor (rachete) având un interval de 200 ... 600 de kilometri, deoarece la aceste distanțe (și) cea mai mare parte din calea proiectilului se extinde în stratosferă, unde rezistența aerului poate fi ignorată. La intervale mai mici, rezistența aerului va influența puternic rezultatul, iar la distanțe mai mari de 600 km gravitația nu mai poate fi considerată constantă.
Exemplul 4. De la un pistol montat la o înălțime h. împușcat sub un unghi la orizont (figura 6). Miezul a zburat din butoiul pistolului la o viteză de u. Definim ecuațiile de mișcare ale nucleului.
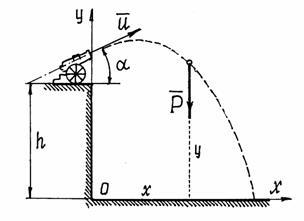
Pentru a compune corect ecuațiile diferențiale de mișcare, trebuie să rezolvăm probleme similare în funcție de o anumită schemă.
a) Atribuiți un sistem de coordonate (numărul axelor, direcția și originea lor). Axele selectate cu succes simplifică soluția.
b) Afișează punctul în poziția intermediară. Ar trebui să se asigure că coordonatele acestei poziții sunt în mod necesar pozitive (figura 6).
c) Afișați forțele care acționează asupra punctului în această poziție intermediară (nu manifestați forțe de inerție!).
În acest exemplu, este doar putere. greutatea miezului. Nu vom lua în considerare rezistența la aer.
d) Se compun ecuații diferențiale în conformitate cu formulele: De aici obținem două ecuații: u.
e) Rezolvați ecuațiile diferențiale.
Ecuațiile obținute aici sunt ecuații liniare de ordinul doi, în partea dreaptă sunt constante. Soluția acestor ecuații este elementară.
Rămâne să găsim constantele integrării. Substituim condițiile inițiale (pentru t = 0 x = 0, y = h,.) În aceste patru ecuații :. . 0 = C2. h = D2.
Substituim valorile constantelor în ecuații și notăm ecuațiile de mișcare ale punctului în forma finală
Cu aceste ecuații, așa cum este cunoscut din secțiunea cinematica poate fi determinată și calea de mișcare a nucleului, iar viteza și accelerația și poziția nucleului, în orice moment dat.
După cum puteți vedea din acest exemplu, schema de rezolvare a problemelor este destul de simplă. Dificultăți pot apărea numai atunci când se rezolvă ecuații diferențiale, ceea ce poate fi dificil.
2) Determinați mișcarea unui punct într-un mod natural.
Modul de coordonate este de obicei determinat de mișcarea unui punct, nelimitat de orice condiții, constrângeri. Dacă mișcarea unui punct este restricționată, viteză sau coordonate, atunci nu este ușor să determinați această mișcare prin metoda coordonatelor. Este mai convenabil să folosiți metoda naturală de specificare a mișcării.
Să determinăm, de exemplu, mișcarea unui punct de-a lungul unei anumite linii fixe, de-a lungul unei anumite traiectorii (figura 7).
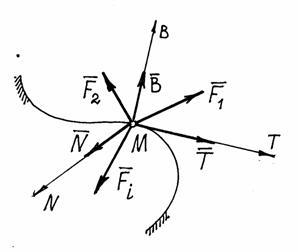
În punctul M, pe lângă forțele active specificate. reacția liniei. Prezentăm componentele reacției de-a lungul axelor naturale
Vom compune ecuația de bază a dinamicii și o vom proiecta pe axele naturale
De atunci obținem ecuații diferențiale de mișcare, cum ar fi
Aici forța este forța de frecare. Dacă linia de-a lungul căreia se deplasează punctul este netedă, atunci T = 0 și apoi a doua ecuație va conține o singură coordonată necunoscută s:
Rezolvând această ecuație, obținem legea de mișcare a punctului. ceea ce înseamnă, dacă este necesar, viteza și accelerația. Prima și a treia ecuație (5) ne vor permite să găsim reacțiile u.
Articole similare
Trimiteți-le prietenilor: