Curbe secundare, elipsă, cerc, parabolă, hiperbolă

Agenția Federală pentru Educație a Federației Ruse

Instituția de învățământ de stat a învățământului superior superior Universitatea de Stat din Ural.

Departamentul de „marfă și examinarea bunurilor de consum“

"Curbe de ordinul doi: o elipsă, un cerc, o parabolă, o hiperbolă"

În disciplina matematică superioară.

Permina Alexandra Nikolaevna

studentul grupului 131

Kravchenko Olga Vladimirovna

Curbe de ordinul doi: o elipsă, un cerc, o parabolă, o hiperbolă.

Curbele de ordinul doi în plan sunt liniile de intersecție a unui con circular cu planuri care nu trec prin vârful lui.

Dacă un astfel de plan intersectează toate generatoarele unei singure cavități conice, atunci se obține o elipsă în secțiune. când generatoarele celor două cavități se intersectează - hiperbola. iar dacă planul secant este paralel cu un generator, atunci secțiunea conului este o parabolă.

Curba de ordinul doi în plan într-un sistem de coordonate dreptunghiular este descrisă de ecuația:

Setul tuturor punctelor de pe planul pentru care suma distanțelor față de două puncte fixe F 1 și F 2 este o constantă dată se numește o elipsă.

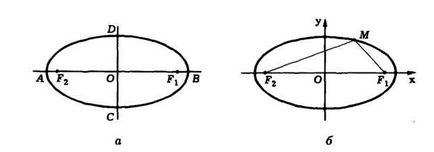
Ecuația canonică a unei elipse.

Pentru orice elipsă, găsim un sistem de coordonate carteziene astfel încât elipsa să fie descrisă de ecuație (ecuația canonică a elipsei):

Descrie o elipsă cu centrul de la origine, ale cărui axuri coincid cu axele coordonatelor. Numărul a este numit axa semimajor a elipsei. iar numărul b este axa semimajor.

• Proprietatea focală. Dacă F1 și F2 sunt focare ale unei elipse, atunci pentru orice punct X aparținând unei elipse, unghiul dintre tangenta în acest punct și linia (F1X) este egal cu unghiul dintre această tangență și linia (F2X).
• O linie dreaptă trasată prin midpoints de segmente tăiate de două linii drepte paralele intersectând elipsa va trece întotdeauna prin centrul elipsei. Acest lucru permite construcția cu ajutorul unei busole și a unei rigle pentru a obține cu ușurință centrul elipsei și mai târziu axe, vârfuri și focare.
• Evoluția elipsei este astroidul.
• Excentricitatea unei elipse este relația. Excentricitatea caracterizează alungirea elipsei. Excentricitatea este mai aproape de zero, elipsa este mai mult ca un cerc și invers, decât excentricitatea este mai aproape de unitate, cu atât mai mult este întinsă.

Elipsa poate fi, de asemenea, descrisă ca

• O figură care poate fi obținută dintr-un cerc prin aplicarea unei transformări afine
• o proiecție ortogonală a cercului pe plan.
• Intersecția unui plan și a unui cilindru circular.

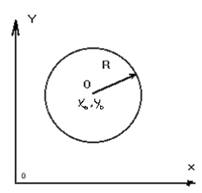
Ecuația canonică a unui cerc.

Ecuația generală a unui cerc este scrisă ca:

Punctul este centrul cercului, R este raza lui.

Ecuația unui cerc de rază R cu centrul la origine:

• O linie dreaptă poate să nu aibă puncte comune cu un cerc; au un punct comun (tangent) cu un cerc; să aibă cu ea două puncte comune (secant).
• Tangenta la un cerc este întotdeauna perpendiculară pe diametrul său, unul dintre ale cărui capete este punctul de tangență.
• Prin intermediul a trei puncte care nu se află pe o linie, puteți desena un cerc și mai mult decât unul.
• Punctul de tangență al celor două cercuri se află pe linia care leagă centrele.
• Lungimea unui cerc cu raza R se poate calcula din formula C = 2π R.
• Unghiul inscripționat este fie jumătate din unghiul central înclinat pe arcul său, fie completează jumătate din acest unghi la 180 °.
  • Două unghiuri inscripționate, susținute de același arc, sunt egale.
  • Unghiul inscripționat, susținut de un arc de jumătate din circumferință, este de 90 °.
• Unghiul dintre două secante trase dintr-un punct situat în afara cercului este egal cu jumătatea diferenței dintre măsurile arcilor situate între secante.
• Unghiul dintre acordurile intersectate este egal cu jumătate de sumă a măsurilor arcului care se află în unghi și arcul opus acestuia.
• Unghiul dintre tangent și coardă este egal cu jumătatea arcului contractat de coardă.
• Segmentele tangentelor la cercul tras dintr-un punct sunt egale și egale cu unghiurile de la linia care trece prin acest punct și centrul cercului.
• Atunci când se intersectează două coarde, produsul segmentelor în care unul este împărțit prin punctul de intersecție este egal cu produsul segmentelor celuilalt.
• Produsul lungimilor de distanțe de la punctul selectat la două puncte de intersecție a cercului și secant care trece prin punctul selectat nu depinde de alegerea secantului și este egal cu magnitudinea absolută a gradului de punct în raport cu cercul.
  Pătratul lungimii segmentului tangent este egal cu produsul lungimilor secțiunilor secantului și este egal cu valoarea absolută a gradului punctului față de cerc.
• Un cerc este o curbă simplă plană a ordinii a doua.
• Un cerc este o secțiune conică și un caz special de elipsă.

O parabolă este un set de puncte pe un plan, fiecare dintre ele fiind la aceeași distanță de un punct dat, numit focalizare și dintr-o linie dată numită directrix și care nu trece prin focalizare.

Ecuația canonică a unei parabole într-un sistem de coordonate dreptunghiulare:

(sau, dacă schimbați axele)

unde p (parametrul focal) este distanța de la focalizare la direcția directoare

• O parabolă este o curbă a ordinii a doua.
• Are o axă de simetrie, numită axa parabolei. Axa trece prin focalizare și este perpendiculară pe regizor.
• Un fascicul de raze paralele cu axa, reflectat într-o parabolă, este colectat în focarul său. Pentru o parabolă cu un vârf la origine (0; 0) și o direcție pozitivă a ramurilor, focalizarea este în punctul (0; 0,25).
• Dacă focalizarea parabolei se reflectă în raport cu tangenta, atunci imaginea va fi regizată.
• O parabolă este un antipod al unei linii.
• Toate parabolele sunt similare. Distanța dintre focalizare și regizor determină scara.
• Când parabola se rotește în jurul axei de simetrie, se obține un paraboloid eliptic.

· O linie dreaptă intersectează o parabolă la cel mult două puncte.

Excentricitatea parabolei e = 1.

Poziția geometrică a punctelor planului pentru care diferența de distanțe față de două puncte fixe este constantă se numește hiperbolă.

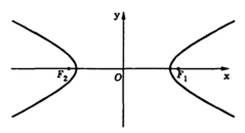
Numerele u sunt numite, respectiv, jumătate de axe reale și imaginare ale hiperboliei.

Hyperbola are două axe de simetrie (axele principale ale hiperbola) și un centru de simetrie (centrul hiperboliei). Una dintre aceste axe intersectează cu hiperbola la două puncte, numite vârfurile hiperboliei. Se numește axa reală a hiperbolei (axa Ox pentru alegerea canonică a sistemului de coordonate). Cealaltă axă nu are puncte comune cu hiperbola și se numește axa imaginară (în coordonatele canonice, axa Oy). Pe ambele părți ale acesteia sunt ramurile dreaptă și stângă ale hiperboliei. Focurile hiperboliei sunt situate pe axa sa reală.

· Fiecare hiperbolă are o pereche de asimptote: și.

· Distanța de la origine la unul dintre punctele focale ale hiperboliei se numește lungimea focală a hiperboliei.

Excentricitatea hiperboliei este cantitatea e = c / a. Excentricitatea hiperboliei e> 1

Distanța de la vârful hiperbolei la asimptotul de-a lungul axei paralele a ordinelor este numită jumătatea axei mici sau imaginare a hiperbolei.

· Distanța de la focalizare la hiperbolă de-a lungul liniei paralele cu axa ordinii se numește parametrul focal.

Trimiteți-le prietenilor: