Din prelegerile noastre
Să presupunem că avem un interval (a. B), în care știm exact că funcția f (x) are un extremum și este 1. În mod similar, funcția este unimodală și diferențiabilă.
Metoda Newton este una dintre metodele care utilizează derivați. De fapt, metoda Newton repetă aceeași metodă de tangente, se aplică doar primelor instrumente derivate.
Construim o funcție f (x) pe intervalul (a, b)
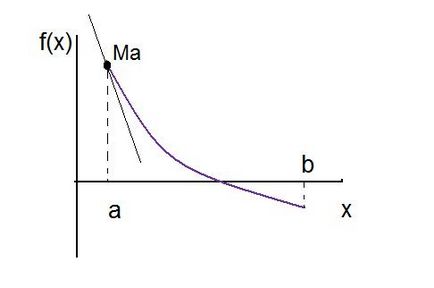
Extindem derivatul funcției din seria Taylor la punctul (x 0, f '(x 0)):
Am aproximative. luând doar primii doi termeni ai seriei:
Prin urmare, obținem asta
Astfel, putem scrie o expresie recursivă:
Această metodă este aplicabilă numai dacă funcția este de două ori diferențiată.
Dacă pe intervalul [a. b] Cel de-al treilea derivat păstrează semnul, apoi:
Ea are o convergență patrată (aceasta este cea mai mare convergență) dacă este îndeplinită condiția de convergență.
Nu există o convergență globală (adică convergența depinde de alegerea punctului de plecare)
La fiecare etapă a metodei, este necesar să se calculeze primul și al doilea derivat.
De pe Internet (în detaliu + dock-va + modificări):
Considerații euristice, care au condus la metoda de optimizare necondiționată a lui Newton.
Dacă vom trece de la faptul că etapa necesară în găsirea soluției problemei
Interpretarea geometrică a formulelor (3) și (4) este prezentată în Fig. 10a și 10b.
Metoda lui Newton se referă la metodele de ordinul doi. deoarece calculul fiecărei iterații necesită cunoașterea celui de-al doilea derivat al funcției f. Din aceleași motive, metoda de gradient se referă la metodele de ordinul întâi. Subliniem că aici nu vorbim despre ordinea de convergență a metodei, ci despre ordinea funcției minimizate utilizată de metoda derivată.
O teoremă asupra convergenței locale superfineare a metodei Newton.
Fie f de două ori continuu diferențiabil și x * un punct staționar nondegenerat. Apoi, există o vecinătate V x * a punctului x * astfel încât aproximările (4). Pornind de la un punct inițial arbitrar x 0 ∈ V x *. sverhlineynoskhodyatsya
Dovada lemnei. Evident, F = f '∈ C1 și prin urmare
Deoarece F '(x *) nu este degenerat. de către (7), pentru x suficient de aproape de x *, operatorul F '(x) este nondegenerat și, în plus,
Prin urmare, în special, pentru x suficient de aproape de x *
Mai mult, deoarece F este diferențiabil și x * este un punct staționar,
(x) - (F) (x) - [F '(x)] -1 F (x) (x) =
= [F '(x)] -1 [F' (x) (x - x *) - F (x)] = o (x - x *).
x n +1 - x * = x n - [F '(x n)] -1 F (xn) - x * # 8797;
# 8797; (Xn - x *) = o (xn - x *).
și, prin urmare, x n → x * ca n → ∞. Mai mult decât atât, pentru un q ∈ arbitrar (0, 1) există a > 0 astfel încât || # 968; (x - x *) || ≤ q || x - x * || pentru || x - x * || ≤ # 949;. Dar atunci, dacă || x n - x * || ≤ # 949; apoi || x n +1 - x * || ≤ q || x n - x * ||. Ultima afirmație presupune în mod evident relația necesară || x n - x * || ≤ Cq n.
Desigur, ca o metodă de ordinul doi. Metoda lui Newton necesită mai multă muncă computațională, deoarece este necesar să se calculeze al doilea derivat al funcției f.
Dacă funcția f este în plus puternic convexă. atunci este posibil să se afirme convergența exact la rezolvarea problemei (1). și nu numai la punctul staționar al funcției f. și, în plus, să estimeze raza vecinătății din care converg apropierea lui Newton.
Teorema privind convergența patratică a metodei Newton.
Să presupunem că f ∈ C 2 și, de altfel, f 'satisface o condiție Lipschitz cu constantă L. Fie f puternică convexă cu o constantă # 955; Fie V x * - cartier de rezolvare a problemei (1). constând din punctele x ∈ Rm astfel încât
În unele probleme, un dezavantaj mai semnificativ al metodei lui Newton este dificultatea computațională mai mare: la fiecare pas este necesar să se calculeze operatorul (matricea) f '' (x n) și inversiunea lui (ei), că pentru dimensiuni mari óeste foarte scump în calcul. O modalitate de a evita aceste dificultăți este de a "îngheța" operatorul f (x n) - folosiți [f (x 0)] -1 în loc de [f (x n)] -1 la fiecare pas:
Interpretarea geometrică a metodei Newton modificată (14) este prezentată în Fig. 12.
Se poate demonstra că, sub constrângeri naturale, metoda Newton modificată converge numai liniar (aceasta este o plată pentru reducerea cantității de calcul). De asemenea, nu puteți îngheța [f '(x n)] -1 pentru totdeauna, dar actualizați-l într-un anumit număr de pași, spune k:
Articole similare
Trimiteți-le prietenilor: