În cazul general, un set de inițial și un set de stări finite ale sistemului
Este necesar să găsim controlul. transferând sistemul de la zonă la zonă pe minut. timp.
În acest caz, pentru a optimiza procesul, este necesar să existe o funcție vectorie continuă care să satisfacă nu numai condiția maximă, ci și condițiile de transversalitate la ambele capete ale traiectoriei (t).
Condițiile de transversalitate constau în vectorul fiind ortogonal la planurile tangente la regiuni și, respectiv, la începutul și la sfârșitul traiectoriei. Vom presupune că funcțiile de restricție sunt continue și continuu diferențiate în raport cu x. Să presupunem de asemenea că domeniile u sunt marcate, închise și convexe.
Să analizăm condițiile în care funcția (t) trebuie să satisfacă dacă punctul inițial aparține regiunii stărilor inițiale, iar punctul final este originea coordonatelor.
pentru că - un set închis, un punct este un punct limită al acestui set: dacă nu ar fi, atunci ar fi nevoie de timp pentru a depăși limitele setului, iar acest lucru nu ar fi optim.
Fie ca punctul inițial al procesului optim. Timpul de la acest punct la cel final. Să construim regiunea de state realizabile corespunzătoare timpului T.
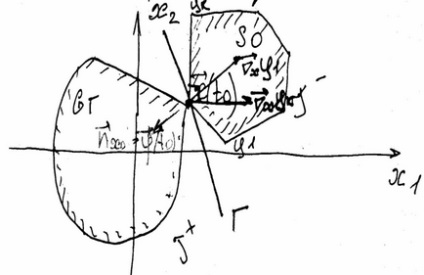
astfel se pare că punctul de plecare este punctul de graniță al două seturi: setul de seturi inițiale și setul de stări atinse în timp T.
Prin teorema lui Hahn-Banach, două seturi convexe și disjuncte pot fi separate de un hyperplane. Dacă aceste regiuni au un punct comun, atunci acest hiperplane este suportul pentru regiuni în acest moment.
Tragem hiperplanul Γ. Dacă hiperplana Γ este privită ca un plan de sprijin pentru regiunea stărilor posibile, atunci normalul către acest hiperplane este vectorul.
Să găsim relația dintre normali și constrângerile: Normalele vor fi direcționate către S0. deoarece
Pentru acele constrângeri care sunt ineficiente de teorema lui Kuhn-Tucker. Apoi, obținem
Dacă mișcarea începe dintr-un punct și se termină într-o zonă, atunci condiția va fi astfel:
Setul acestor două condiții este numit condiția de transversalitate.
Notă: dacă regiunea finală este un punct, atunci este aleasă arbitrar. Dacă aria țintă este întregul spațiu de fază, atunci = 0, deoarece toți coeficienții vor fi zero (și toate restricțiile, respectiv, sunt ineficiente).
8. Principiul maxim pentru problemele de control ale sistemelor staționare cu un criteriu de calitate integrat.
Sarcinile de management cu un criteriu de calitate integrat:
Funcția L este continuă în argumentele sale și are derivate parțiale continue. Dacă funcția L = 1, atunci problema de viteză optimă.
Condiția principiului maxim pentru sistemele staționare:
Sarcinile de management cu un criteriu de calitate integral, atunci când funcționalitatea, aria țintă și ecuația de stat nu depind în mod explicit de timp.
Fie ca starea unui sistem dinamic să fie descrisă printr-o diferență neliniară. ecuația formei :.
Având în vedere o regiune. starea inițială S0 și sf. Este necesar să se stabilească condițiile, pisica. Satisfăcătoare. Controlul optim din regiunea admisibilă și o traiectorie corespunzătoare unui control optim, care satisface condițiile limită.
.
Presupunem că timpul final t nu este specificat.
Să presupunem că L nu depinde în mod explicit de timp și este pozitiv.
Trecem de la un timp real la un moment fictiv. Cu acest lucru în minte, diferă sistemul original. va lua forma:. (). Apoi funcțional ia forma: (*) - redusă la problema vitezei optime.
Să transferăm condițiile obținute pentru probleme de performanță optime într-o clasă mai mare de probleme. Fie () un proces optim în sensul formulei (*), atunci satisface principiul maxim pentru problema optimă a vitezei.
Există o funcție, rel. pisică. Voi. condiții:; unde
Condiția maximă este satisfăcută:
Pe parcursul traiectoriei optime, funcția hamiltoniană are următoarea formă:
Condiția de transversalitate este îndeplinită.
Introducem funcția de structură, înlocuim ecuația lui Hamilton (1)
(2) Se numește această funcție. Hamiltonianul unui sistem cu un criteriu de calitate integral. Hamiltonian = 0 numai de-a lungul traiectoriei optime. În cazul general, atunci când nu există dependență de timp: (3).
Introducerea Hamiltonianului ne permite să generalizăm condiția maximă, adică putem spune că dacă () -opt. proces, trebuie îndeplinite următoarele condiții:
Trebuie să existe o funcție pentru pisică. traseul este corect. corelația: a); b)
Condiția maximă este satisfăcută:
Hamiltonian de-a lungul traiectoriei optime = 0.
Condiția de transversalitate este îndeplinită.
Să trecem de la timpul condiționat la timpul real t:
,- Condiția 1a este îndeplinită.
Verificăm (1b) :, trecem de la kt :, - condiția 1b este satisfăcută.
Verificăm condițiile. 2 :, prin urmare,
Cond. 3: Hamiltonian de-a lungul opt. traiectorie = 0, aceasta rezultă din derivarea sa și se bazează pe condiția 2
Cond. 4: Pentru că în condiția de transversalitate nici Hamiltonianul, nici Hamiltonianul nu sunt incluse, ele sunt complet conservate. genul său:
Observația1: Am obținut condiția max în ipoteza că, dar sunt, de asemenea, mulțumiți în cazul general.
Notă2: ConstP0 este de obicei presupus a fi -1. P0 = -1
Articole similare
Trimiteți-le prietenilor: