Aceasta înseamnă că seturile infinite A și B sunt echivalente, AăttB. au aceeași putere. Este interesant că în acest caz setul A este echivalent cu subsetul său B, A
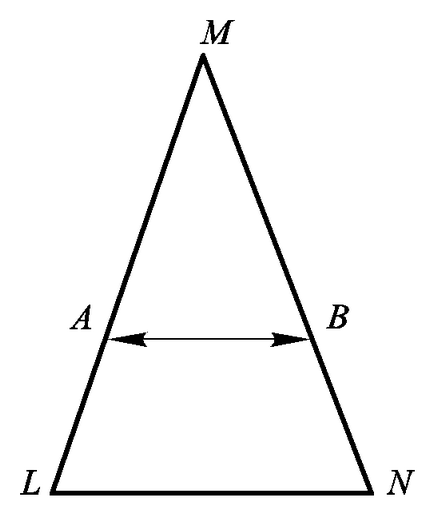
Fig. 7.6. Stabilirea unei corespondențe unu-la-unu între părțile egale ale unui triunghi isoscel.
2. LM și NM să fie laturi egale ale unui LMN triunghi isoscel (Figura 7.6).
Prin conectarea punctelor A și B la laturi egale ale unui triunghi prin segmente de linii drepte paralele cu baza LN. obținem o corespondență unu-la-unu între punctele seturilor definite de segmentele LM și NM. În consecință, aceste seturi sunt echivalente și au aceeași putere.
3. Acum permiteți LN și MN să fie laturile inegale ale LMN triunghi (vezi Figura 7.7). Conectând punctele A și B pe aceste laturi prin segmente de linii drepte paralele cu partea laterală LM. constatăm că laturile inegale definesc seturi de puncte de aceeași culoare. Ideea este
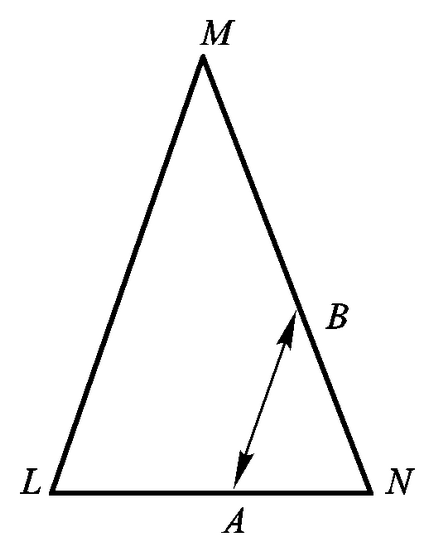
Fig. 7.7. Stabilirea unei corespondențe unu-la-unu între laturile inegale ale unui triunghi isoscel.
Faptul că laturile LN și MN au lungimi diferite, dar fiecare dintre ele conține un număr infinit de puncte, care sunt la fel de "multe".
Seturi de calculatoare
Apelam setul ACCOUNT. dacă este echivalent cu setul de numere naturale.
Astfel, abilitatea de a "număra" toate elementele dintr-un set determină contabilitatea sa. Această sarcină este departe de a fi întotdeauna ușoară.
Observăm câteva proprietăți ale mulțimilor numărabile.
1. Din orice set infinit se poate alege întotdeauna un set de numărare.
Într-adevăr, dacă setul A este infinit, atunci mulțimea numărabilă N poate fi construită după cum urmează. Selecem ca primul element al setului N, de exemplu, elementul setului A. Deoarece A este infinit, eliminarea unui element din el își va păstra infinitatea. Apoi, separăm elementul de setul rămas prin adăugarea lui la setul N. apoi dintr-un set infinit separăm elementul prin atașarea lui la N și așa mai departe. Setul N ia forma: și va fi numărare.
Dați un exemplu care ilustrează această proprietate.
2. Fiecare subset infinit al unui set de numărare poate fi de asemenea numărare.
Dacă mulțimea A este numărabilă și B este subsetul său infinit, atunci listarea secvențială a elementelor setului A. vom întâlni elementele setului B și numărăm ele, adică elementele setului B. B

3. Unirea oricărui set de mulțimi finite sau numărabile de seturi numărabile este un set numerotabil.
Pentru a demonstra această proprietate, considerăm seturi numărare:
Formăm un nou set de seturi
Se formează astfel încât la început elementul să fie localizat, atunci există elemente pentru care suma indicilor este de 3. potom4. și așa mai departe. Un astfel de set cuprinde toate elementele setului în sine, numărare, echivalentă cu N.
Puterea continuă
Având în vedere proprietățile seturilor numărabile, am încercat să demonstrăm echilibrarea anumitor seturi infinite. Dar toate seturile infinite sunt numărate? Pentru a găsi nenumărate seturi, multe dificultăți trebuiau să fie depășite. Atât Bolzano cât și G. Cantor, simțindu-se că ideea de a stabili o corespondență unu-la-unu este cheia pentru găsirea puterii seturilor infinite, au fost aproape de rezolvarea problemei simultan. B. Bolzano a venit pentru prima dată la metoda de estimare a mulțimilor infinite prin stabilirea unei corespondențe unu-la-unu, iar G. Cantor a fost primul care a găsit un set nesemnificativ. Este infinit și nu este echivalent cu setul de numere naturale.
Teorema. Un segment al unei linii de numere conține un set nesemnificativ de puncte.
(O altă modalitate de a demonstra această teoremă, "metoda diagonală Cantor", este dată în Anexă)
Să presupunem contrariul: - un set numeric de puncte. Le numerotăm:
Are vreun punct al acestui segment să fie inclus în această secvență?
Pentru a demonstra teorema, este necesar să găsim un punct pe un interval care nu este închis de o secvență dată.
Pentru a face acest lucru, împărțiți segmentul în trei părți egale (Figura 7.8). Obținem segmentele:
Fig. 7.8. Construcția unui punct care nu este în secvență.
De ce se divide în 3 părți, și nu în jumătate sau în 4 părți? De ce ar trebui aceste trei părți să fie egale?
Cel puțin unul dintre ei nu are nici un punct. Selectați-l, împărțiți noul segment, care este un subset al segmentului, din nou în trei părți egale și selectați cel în care nu există nici un punct (în acest al treilea nu vor exista nici puncte, nici puncte, după cum sa stabilit mai sus). Apoi divizăm noul segment în trei părți egale și alegem unul dintre ele, unde nu există nici un punct a3 (după cum se arată, nu vor exista puncte sau nu) și așa mai departe. În consecință, la următoarea etapă obținem un segment de lungime pe care nu există nici un punct, ... Continuând acest proces infinit, găsim un punct. care nu este inclus în secvență
Într-adevăr, a este punctul comun al acestor segmente. Fiind un punct al unui segment, el trebuie să intre în secvența indicată, dar acest lucru este imposibil, pentru că indiferent de n luăm, punctul a nu poate aparține segmentului corespunzător, iar punctul a va aparține acestuia, prin urmare, a este diferit de întregul an. ceea ce dovedește teorema.
Cardinalitatea seturilor echivalente cu un interval se numește capacitatea continuumului și este notată cu litera c.
Indicăm câteva dintre aceste seturi.
Luați în considerare segmentul. Formula de mai jos
,
stabilește o corespondență unu-la-unu între set și set. Prin urmare, are cardinalitatea continuumului.
În plus, seturile:
au aceeași putere a continuumului c. deoarece acestea diferă de set printr-un număr finit de puncte, ceea ce le economisește puterea.
Un rezultat complet neașteptat a fost obținut de G. Cantor, presupunând inițial că pătratul cu partea egală cu 1. conține mai multe puncte decât segmentul. S-au dovedit a fi echivalente.
"Văd asta, dar nu-mi vine să cred", a scris el într-o scrisoare către Dedekind.
Într-adevăr, dacă pătratul este localizat în sistemul de coordonate XOY. după cum se arată mai jos. 7.9. apoi fiecare dintre punctele sale interioare. având coordonate
este posibil să se pună în corespondență un punct dintr-un interval:
Diferitele puncte ale intervalului vor corespunde diferitelor puncte W ale pătratului. Se poate demonstra (folosind argumente mai riguroase) că o astfel de corespondență unu-la-unu va fi una la una, deci setul de puncte dintr-un pătrat cu o latură egală cu 1. și segmentul au aceeași putere. În plus, nu numai un pătrat, ci, de exemplu, un cub sau o minge, conține "cât mai multe" puncte ca și segmentele.
O comparație a setului de numere naturale care este numărabilă și un set nesemnificativ de puncte dintr-un segment ridică întrebarea: există seturi de putere intermediară? Cu alte cuvinte, există un set infinit în care numărul de elemente este "mai mare" decât numerele naturale și "mai puțin" decât punctele dintr-un segment? Aceasta este faimoasa problemă a lui CONTINUUM. care încă excitează mulți matematicieni. La începutul anilor șaizeci
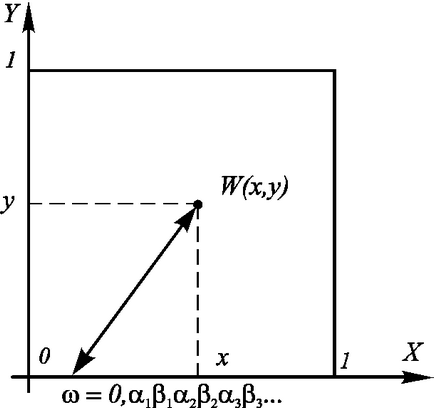
Fig. 7.9. O corespondență unu-la-unu între punctele din interiorul pătratului și punctele din interval.
Secolul al XX-lea sa stabilit că există ambele sisteme axiomice în care ipoteza continuumului este adevărată și construcții axiomatice în care este falsă.
În teoria seturilor, se demonstrează următoarele afirmații:
Pentru orice set A există un set de puteri mai mari (vezi 2 și 3).
Nu există seturi cu cea mai mare putere. (vezi 3).
Setul tuturor submulțimilor lui A are o putere mai mare decât cardinalitatea A.
Setul tuturor subseturilor dintr-un set numărare are cardinalitatea continuumului.
Teoria seturilor este plină de probleme și de paradoxuri. care sunt în prezent de interes pentru cercetători. Una dintre cele de mai sus este discutată mai sus. Aici oferem paradoxul clasic B. Russell.
Fie M setul tuturor mulțimilor și N mulțimea tuturor subseturilor. Apoi cardinalitatea setului N al tuturor subseturilor trebuie să fie mai mare decât cardinalitatea setului M (prin propoziția 3). Dar, prin definiție, N este un subset, deci N = M. Avem o contradicție inevitabilă.
Articole similare
Trimiteți-le prietenilor: