Oscilațiile amortizate sunt oscilații a căror energie scade cu timpul. Procesul extrem de durabil al speciilor în natură este imposibil. Oscilațiile libere ale oricărui oscilator devin mai curând sau mai târziu umezite și încetează. Prin urmare, în practică, ele se ocupă de obicei de oscilații amortizate. Acestea se caracterizează prin faptul că amplitudinea oscilațiilor A este o funcție descrescătoare. De obicei, amortizarea are loc sub acțiunea forțelor de rezistență ale mediei, cel mai adesea exprimată de o dependență liniară de viteza oscilațiilor sau de pătratul acesteia.
Să existe un sistem alcătuit dintr-un izvor (respectând legea lui Hooke), un capăt al căruia este fixat rigid, iar celălalt este un corp de masă m. Oscilațiile se fac într-un mediu în care forța de rezistență este proporțională cu viteza cu un coeficient c (vezi frecare vâscoasă).
A doua lege a lui Newton pentru sistemul în cauză este scrisă după cum urmează:
unde este forța rezistenței, este forța elastică
sau în formă diferențiată
unde k este coeficientul de elasticitate din legea lui Hooke, c este coeficientul de rezistență, care stabilește relația dintre viteza de deplasare a greutăților și forța de rezistență rezultată.
Pentru simplitate, se introduce următoarea notație:
Cantitatea se numește frecvența naturală a sistemului, coeficientul de atenuare.
Apoi ecuația diferențială ia forma
După ce a făcut un înlocuitor. ecuația caracteristică
Ale căror rădăcini sunt calculate conform următoarei formule
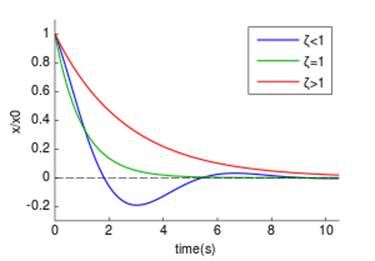
Dependența curbelor de oscilație de valoarea.
În funcție de mărimea coeficientului de atenuare, soluția este împărțită în trei variante posibile.
În cazul în care. atunci există două rădăcini reale, iar soluția ecuației diferențiale ia forma:
În acest caz, oscilațiile se diminuează exponențial încă de la început.
În cazul în care. două rădăcini reale coincid. iar soluția ecuației este:
În acest caz, poate exista o creștere temporară, dar apoi o decădere exponențială.
În cazul în care. atunci soluția ecuației caracteristice este două rădăcini complexe conjugate
Apoi soluția ecuației diferențiale inițiale este
Unde este frecvența naturală a oscilațiilor amortizate.
Constantele și în fiecare dintre cazuri sunt determinate din condițiile inițiale:
Atenuarea oscilațiilor este atenuarea treptată a oscilațiilor în timp, cauzată de pierderea energiei de către sistemul oscilator. Legea amortizării oscilațiilor depinde de proprietățile sistemului oscilator. Sistemul este numit liniar. dacă parametrii care caracterizează proprietățile fizice esențiale ale sistemului în procesul în cauză nu se modifică în timpul procesului. Oscilațiile libere de amortizare ale unui sistem liniar sunt descrise de ecuația:
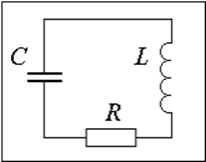
Se introduce o soluție pentru a rezolva ecuația (7.1.1). Această substituire conduce la ecuația caracteristică:
care are două rădăcini:
Dacă atenuarea nu este prea mare (la), radicandul va fi negativ. Dacă este prezentat în formular. unde este o cantitate reală pozitivă, numită frecvența ciclică a oscilațiilor amortizate și este egală cu. atunci rădăcinile ecuației (3) pot fi scrise sub forma:
Soluția generală a ecuației (7.1.1) este funcția:
care pot fi reprezentate ca:
Aici și sunt constante arbitrare.
În conformitate cu (7.1.6), mișcarea sistemului poate fi considerată condițional ca o oscilație armonică a frecvenței w cu o amplitudine care variază în conformitate cu legea:
Rata de amortizare a oscilațiilor este determinată de coeficientul de amortizare. Conform expresiei (7.1.7), coeficientul de atenuare este invers în magnitudine față de intervalul de timp pe care amplitudinea oscilațiilor scade în "e" = 2.718 ori.
Perioada de oscilații amortizate
Perioada de oscilații amortizate este determinată de formula:
Cu o amortizare nesemnificativă (), perioada de oscilații este practic egală. Pe măsură ce perioada crește, perioada crește. Din relația (7.1.7) rezultă că. Acest raport de amplitudini este denumit decrement de amortizare. iar logaritmul său natural este scăderea logaritmică a amortizării:
Reducerea logaritmică a amortizării este inversă în mărime față de numărul de oscilații efectuate în timpul în care amplitudinea scade cu "e" ori. Pe lângă cantitățile considerate, o cantitate este utilizată pentru a caracteriza sistemul oscilator. numit factorul Q al sistemului oscilator. Factorul Q este proporțional cu numărul de oscilații realizate de sistem în timpul în care amplitudinea oscilațiilor scade ori "e". O atenuare mică corespunde valorilor mari ale factorului de calitate. Energia sistemului oscilator scade cu timpul. Acest lucru se datorează prezenței atenuării. Cu o mică amortizare, atunci când energia variază în conformitate cu legea:
unde este valoarea energetică la momentul inițial.
Se poate demonstra că, cu o amortizare slabă, factorul Q la un factor de 2 p este egal cu raportul dintre energia stocată în sistem într-o anumită perioadă de timp și scăderea acestei energii într-o singură perioadă de oscilație.
Cu creșterea g, perioada de oscilație crește. Când perioada se transformă în infinit, adică mișcarea încetează să mai fie periodică. Cu sistemul retras din poziția de echilibru, se întoarce la el fără oscilație.
Cu o amortizare nesemnificativă (), perioada de oscilații este practic egală. Pe măsură ce perioada crește, perioada crește. Din relația (7.1.7) rezultă că. Acest raport de amplitudini este denumit decrement de amortizare. iar logaritmul său natural este scăderea logaritmică a amortizării:
Trimiteți-le prietenilor: