Arborele segmentelor 1

definiție

Un arbore segment este o structură de date care vă permite să efectuați mai multe operații cu segmente ale unui tablou pentru $ O (\ log N) $. Un arbore al segmentelor este o structură de date universală pentru care puteți implementa un set nelimitat de operații (uneori pentru o complexitate mai mare: $ O (\ log ^ 2N) $). Cea mai simplă versiune a arborelui segmentelor vă permite să găsiți suma sau minimul pe o linie și să schimbați elementele individuale.

Construirea unui copac de segmente

Un arbore al segmentelor este un arbore binar complet în care fiecare vârf este responsabil pentru un segment din matrice. Rădăcina copacului este responsabilă pentru întreaga matrice, pentru cele două vârfuri ale copilului - pentru cele două jumătăți și așa mai departe. Fiecare vârf care corespunde unui segment de lungime mai mare de $ 1 $ are două vârfuri copil, care sunt responsabile pentru jumătățile stângi și drepte ale acestui segment. Frunzele copacului segmentelor sunt responsabile pentru elementele individuale (segmente de lungime $ 1 $).

Din punct de vedere grafic, aceasta arată (pentru o serie de 8 elemente):

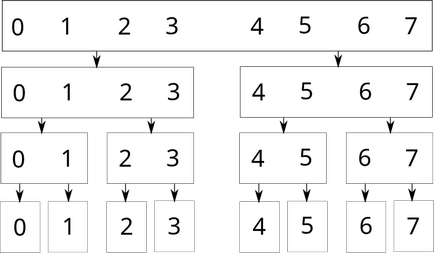
Fiecare dreptunghi este vârful arborelui de segmente. Dacă unele nod este responsabil pentru durata de lungime impar, atunci unul dintre nodurile sale copil va fi responsabil pentru un segment de lungime $ \ lceil \ rceil $, iar celălalt - pentru lungimea de $ segment \ lfloor \ rfloor $. De exemplu, arborele segmentelor pentru o serie de 13 elemente arată astfel:

Pentru o serie de elemente $ n $, arborele segmentelor are aproximativ $ 2n $ vertices ($ n + + + \ ldots $), iar înălțimea lui este de ordinul $ \ log n $.

Principalele segmente ale proprietății copac, pe care sunt construite toate algoritmii lucra cu el orice segment continuu în matrice de $ n $ elemente pe care pot fi reprezentate de aproximativ 2 $ \ log n $ noduri pe segmentele de copac.

De exemplu, segmentul $ [1; 11] într-o matrice de lungime de 13 $ poate fi reprezentată folosind următoarele noduri:

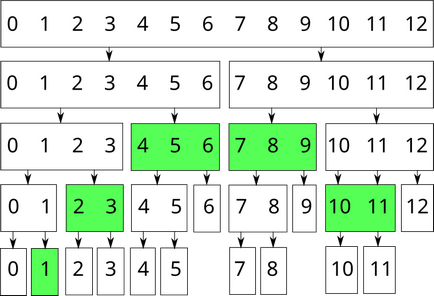
Un arbore de segmente pentru a găsi suma

Una dintre cele mai simple funcții care pot fi considerate $ O (\ log N) $ folosind arborele de segmente este suma.

Atunci când construim un copac la fiecare dintre vârfurile sale, salvăm suma pe segmentul corespunzător (construcția va fi recursivă, deci este suficient să adăugăm sumele pe două segmente de copil). Apoi, fiecare solicitare pentru o sumă pe un segment va fi împărțită în segmente de $ 2 \ log N $ și veți găsi suma pentru fiecare dintre acestea pentru $ O (1) $ folosind valorile prezise. Astfel, complexitatea interogării sumei este $ O (\ log N) $.

În plus față de interogarea sumelor arborelui de segmente, pot exista, de asemenea, cereri de modificare a elementelor individuale (modificare). Rețineți că, din schimbarea unui element, valoarea sumei se schimbă într-un vertex la fiecare nivel al arborelui segmentului (în care intră acest element). Recalculați valorile sumei (din nou, recursiv) numai la aceste noduri. Astfel, complexitatea cererii de modificare este egală cu înălțimea arborelui, sau $ O (\ log N) $.

Pentru a implementa o interogare sumă și o cerere de modificare, este implementat un traversal arbore folosind același algoritm bazat pe DFS. Permiteți granița interogării noastre $ [L; R] $ (în cazul unei cereri de modificare $ L = R $) și limita segmentului corespunzător vârfului curent $ [TL; TR] $. În funcție de poziția reciprocă a acestor limite, există trei opțiuni pentru algoritm:

Segmentul curent este complet inclus în interogare ($ L \ le TL; TR \ le R $).

Dacă aceasta este o solicitare pentru o sumă, returnați suma preplătită pe interval. Dacă aceasta este o cerere de modificare, schimbați elementul și recalculați suma. Nu este nevoie să mergeți la summiturile copiilor.

Segmentul curent nu este complet inclus în interogare ($ TR

Nu este nevoie să efectuați nicio acțiune, trebuie doar să renunțați la această funcție. Dacă este vorba despre o sumă, returnați $ 0 $.

Segmentul curent face parte din interogare.

Apelați funcția recursiv pentru două segmente de copil. Dacă aceasta este o sumă, returnați suma celor două valori. Dacă aceasta este o cerere de modificare, recalculați valoarea sumă pentru segmentul curent (deoarece s-ar fi putut modifica).

Să desemnați aceste variante în mod corespunzător culoarea verde, roșie și galbenă. Apoi, interogarea sumei din intervalul $ [1; 11] $ matrice de $ 13 $ lungime va fi procesată după cum urmează: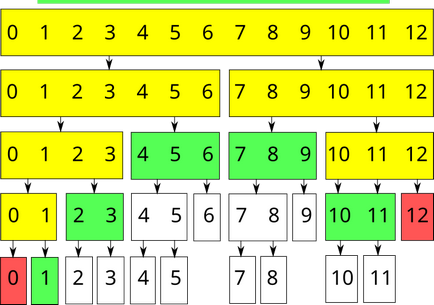

O solicitare de modificare a elementului $ 4 $ th:

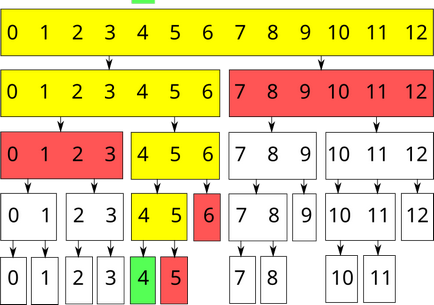
Implementarea arborelui de segmente pentru a găsi suma

Reprezentăm un arbore binar complet, ca într-o lecție despre o grămadă, folosind o matrice și formule de tranziție $ l = 2v $ și $ r = 2v + 1 $. Pentru a preveni toate depășirile posibile, mărimea arborelui segmentului pentru o matrice de elemente $ n $ este presupusă a fi $ 4n $.

Implementarea în C ++:

Implementarea unui arbore de segmente pentru a găsi minimul

Pentru a găsi minimul, trebuie să modificați doar câteva rânduri în implementarea anterioară:

Copaci de segmente, păstrând toate elementele

Pentru a rezolva unele probleme, vârful responsabil pentru segment trebuie să stocheze toate elementele acestui segment în ordinea de sortare. Se pare că va dura prea multă memorie, dar nu este. Fiecare element al matricei este stocat o dată la fiecare nivel al arborelui, care este $ \ log n $. Prin urmare, întreaga structură de date suportă $ O (N \ log N) $ de memorie.

Problema clasică pentru un copac de astfel de segmente este următoarea:

Având o serie de numere de $ N $, care primește interogări $ M $. Solicitările au forma $ (l, r, x) $. Pentru fiecare cerere, trebuie să răspundeți câte elemente mai mari sau egale cu $ x $ sunt conținute pe segmentul $ [l; r] $.

Pentru a rezolva această problemă, stocăm vectorul std :: sortat la fiecare vârf al arborelui segmentului. conținând toate elementele segmentului corespunzător. Pentru a răspunde la interogare, vom folosi funcția std :: lower_bound. Vă permite să răspundeți la o interogare pentru un vertex pentru $ O (\ log N) $, deci complexitatea totală a răspunsului la interogare va fi $ O (\ log ^ 2N) $.

Implementarea în C ++:

Dacă în astfel de sarcini este permisă modificarea elementelor, atunci în loc de std :: vector este necesar să stocăm std :: multiset. care vă permite să eliminați rapid și să adăugați elemente. Dar în acest caz nu mai putem răspunde la cererile pentru numărul de elemente, deoarece iteratorii std :: multiset nu pot fi separați.

Un copac de segmente cu o actualizare masivă. Neconcordate subtrees

Datorită unei anumite modificări, arborele segmentelor poate actualiza elemente (creștere sau atribuire) pe segmente de lungime arbitrară pentru $ O (\ log N) $. Această modificare este destul de generală și vă permite să rezolvați o întreagă clasă de sarcini noi utilizând arborele de segmente.

Ideea este asta. Să presupunem că, în timpul executării cererii de alocare pe segment, am coborât la vârful care aparține integral acestui segment. În mod logic, trebuie să schimbăm valoarea în acest vârf și în toate nodurile subtreei sale. Dar complexitatea unei astfel de operațiuni este inacceptabil de mare: $ O (N \ log N) $.

În schimb, vom proceda după cum urmează: schimba valoarea numai foarte sus, fără a actualiza subarborele sau (astfel, în subarborele valori incorecte depășite sunt acum stocate), și amintiți-vă că acest vârf are modificări necoordonat. Acest lucru completează interogarea pentru vârful și subdria lui.

Dacă cererile ulterioare nu accesează un subrubric cu o modificare inconsistentă, acestea vor fi executate corect. Dar, mai devreme sau mai târziu, se poate primi o cerere, care trebuie procesată individual pentru vârfurile copilului cu o modificare necoordonată. În acest caz, procedăm pur și simplu: trecem modificarea la vârfurile copilului (numai la vârfurile copilului și nu la întregul substrat). Acum, acest vertex este de acord, iar inconsistența a trecut la copiii săi. Această operație se numește împingând modificarea.

Probabil, numai vârfurile copilului au fost obligate să proceseze cererea și o singură împingere va fi suficientă. Dacă interogarea va fi coborâtă în jos subtree, pe măsură ce coborâm, vom împinge modificarea din ce în ce mai mică. Împușcarea este efectuată pentru $ O (1) $ în același timp cu interogarea este împărțită, astfel încât aceasta nu afectează comportamentul asimptotic.

De exemplu, hai să lucrăm cu arborele de segmente pentru a găsi suma cu alocare de masă. Am atribuit un segment $ [0; 6] $ valoarea $ x $. Să modificăm valoarea sumei la vârful care corespunde acestui segment (setați-l la 7x $) și setați parametrul de modificare neregulat pentru acest vârf la $ x $.

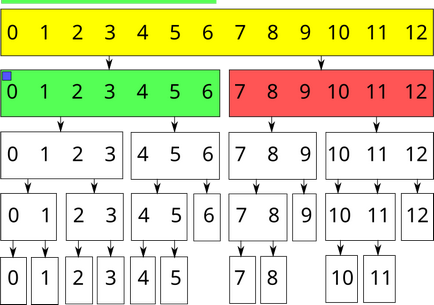
Un pătrat albastru indică prezența unei modificări necoordonate la vârf.

Acum procesăm interogarea pentru găsirea sumei pe intervalul $ [6; 7] $:

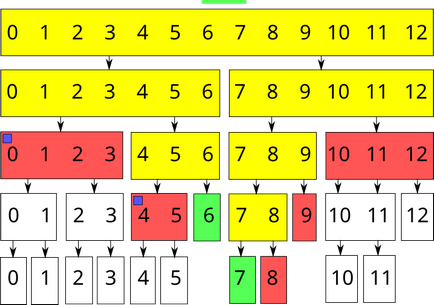
După cum puteți vedea, inconsistența a trecut pe segmentele $ [0; 3] $ și $ [4; 5] $. Aceasta ar trece la segmentul $ [6; 6] $, dar nu are vârfuri de copil, astfel încât inconsistența este eliminată.

Implementarea unui arbore de segmente pentru a găsi o sumă cu alocare de masă

Articole similare

Pagina anterioară

Pagina următoare