§ 19. Arctangent și arccotangent. Soluția ecuațiilor tgx = a, ctgx = a
În exemplul 2 din § 16 nu am putut rezolva trei ecuații:
Doi dintre ei au decis deja - primul în § 17 și § 18 în al doilea, de a face acest lucru a trebuit să introducem conceptul de arccosinusului și arcsinus. Luați în considerare a treia ecuație x = 2.
Funcții Charts = tg y x = 2 și y au infinit mai multe puncte în comun, abscisa tuturor acestor puncte sunt de forma - abscisa punctului de intersecție al liniei y = 2 cu principalele tangensoidy ramură (Figura 90.). Pentru numărul x1 matematicienii au venit cu notația arctg 2 (citiți "arctangent of two"). Apoi toate rădăcinile ecuației x = 2 pot fi descrise de formula x = arctg2 + nk.
Ce este arctg 2? Acesta este un număr al cărui tangent este de 2 și care aparține intervalului
Considerăm acum ecuația tan x = -2.
Graficele funcții au infinit mai multe puncte în comun, abscisa toate aceste puncte au forma abscisa punctului de intersecție al liniei y = -2 tangensoidy ramura principală. Pentru numărul x2, matematicienii au venit cu notația arctg (-2). Apoi, toate rădăcinile ecuației x = -2 pot fi descrise de formula
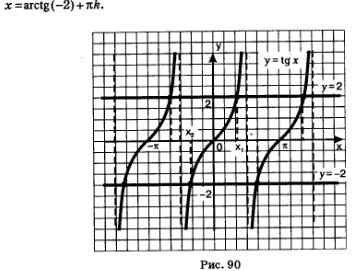
Ce este arctg (-2). Acesta este un număr al cărui tangent este -2 și care aparține intervalului. Observați (vezi Figura 90): x2 = -x2. Aceasta înseamnă că arctg (-2) = - arctg2.
Să formuleze definiția arcului tangent în formă generală.
Definiție 1. arctg a (arctangent a) este un număr din interval. a cărui tangenta este egală cu a. Și așa,
Acum suntem în poziția de a trage o concluzie generală despre soluția ecuației x = a: ecuația x = a are soluții
Deasupra am observat că arctg (-2) = -arg2. În general, pentru orice valoare a unei formule
Exemplul 1. Se calculează:

Exemplul 2. Rezolvarea ecuațiilor:
Soluția: a) Să formulăm formula soluției:
Nu putem calcula valoarea tangentei arc în acest caz, deci lăsăm notația soluțiilor ecuației în forma obținută.
răspundă:
Exemplul 3. Rezolvarea inegalităților:
Inegalitatea speciei poate fi rezolvată grafic, urmând următoarele planuri
1) construiți un tangentoid y = tan x și o linie dreaptă y = a;
2) să aloce pentru ramura principală a tangoidelor un interval al axei x pe care este îndeplinită inegalitatea dată;
3) luând în considerare periodicitatea funcției y = tan x, scrieți răspunsul într-o formă generală.
Aplicăm acest plan la rezolvarea anumitor inegalități.
Soluția. a) Construim graficele funcțiilor y = tan și y = 1. Pe ramura principală a tangentei, se intersectează într-un punct
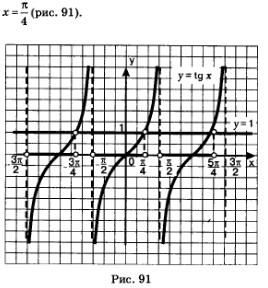
Eliminăm intervalul axei x, pe care ramura principală a tangenteidului este situată sub linia dreaptă y = 1, este intervalul
Având în vedere periodicitatea funcției y = tan, concluzionăm că inegalitatea dată se află pe orice interval de formă:
Unirea tuturor acestor intervale este soluția generală a inegalității date.
Răspunsul poate fi scris în alt mod:
b) Construim grafice ale funcțiilor y = tan x și y = -2. Pe ramura principală a tangenteidelor (Figura 92) se intersectează la punctul x = arctg (-2).
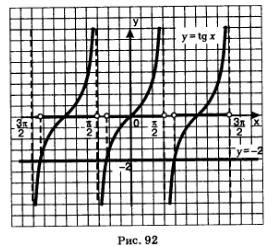
Eliminăm intervalul axei x, în care ramura principală a tangentei
Luați în considerare ecuația cu tan x = a, unde a> 0. Graficele funcțiilor y = CTG x și y = o infinitate de puncte comune, abscisa tuturor acestor puncte sunt de forma: x = x1 + nk unde x1 = agsstg și - abscisa punctului de intersecție al liniei drepte y = a cu principalele tangensoidy ramură (Figura 93. ). De aici agsstg a - este un număr care este egal cu cotangentă unei și care aparține intervalului (0, n); acest interval este construit ramura principală a graficului y = x CTG.
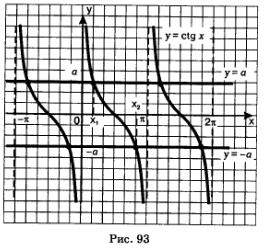
În Fig. Figura 93 prezintă, de asemenea, o ilustrare grafică a soluției din ecuația dtg = -a. Funcții Grafice CTG y = x și y = -a sunt infinit de multe puncte comune, abscisa tuturor acestor puncte sunt de forma x = x2 + nk unde agsstg x2 = (- a) - abscisa punctului de intersecție al liniei y = -a o tangensoidy principală ramură . De aici agsstg (e) - este un număr care este egal cu cotangentă specificat și care aparține intervalului (O, n); pe acest interval este construită ramura principală a graficului funcției V = ctg x.
2. Determinarea agsstg a (cotangentă inversă a) - a este un număr în intervalul (0, n), care este egal cu cotangentă unei.
Și așa,
Acum suntem în poziția de a face o concluzie generală despre soluția ecuației ctg x = a: ecuația ctg x = a are soluții:
Observați (vezi Figura 93): x2 = n-x1. Asta înseamnă că
Exemplul 4. Se calculează:
Soluția este: a)
Ecuația ctg x = a poate fi aproape întotdeauna transformată în formă O excepție este ecuația ctg x = 0. Dar în acest caz, profitând de faptul că puteți merge la
ecuația cos x = 0. Astfel, o ecuație a formulei x = a nu reprezintă un interes independent.
AG Mordkovich clasa Algebra 10
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.
Articole similare
Trimiteți-le prietenilor: