Modelul 1. Sistemul postulatelor lui Euclid
Postulate 1-3 determină posibilitatea de a construi o riglă (fără diviziuni) și o busolă. Este util să clarificăm că Euclid "direct" înțelege linia dreaptă "mărginită", adică, în terminologia modernă, un segment.
Matematicienii au apelat în mod repetat la sistemul de postulate și axiome al lui Euclid, încercând să-l îmbunătățească. Deci, în secolul al XVIII-lea. sa constatat că postulatul 4 este inutil, deoarece rezultă din alte postulate și axiome.
Studii similare au fost efectuate pentru o lungă perioadă de timp și postulatul 5-lea, în plus, că este din cauza complexității limbajului au apărut mult mai puțin evidente decât celelalte postulate și axiome. El a încercat să dovedească, pe baza celorlalte postulate și axiome. În acest caz, doar pentru a afla că a 5-a postulat este logic echivalentă cu o altă afirmație (adică, ele pot fi derivate din acesta, iar pe de altă parte, el poate fi derivat din oricare dintre ele, dacă presupunem că ei au stabilit deja), dar nici el , și nici aceste declarații nu pot fi dovedite pe baza altor postulate și a axiomelor lui Euclid. geometria imaginabil, în care 5-lea postulat nu este îndeplinită, iar postulate rămase și axiome sunt îndeplinite (geometria Lobachevsky). De obicei, într-un cont modern, geometria cincilea postulat se înlocuiește cu postulatul echivalent paralel (deja găsite în Proclus în secolul V î.Hr. ...) Printr-un punct nu pe o anumită linie, puteți desena doar o singură linie dreaptă, care nu se intersectează cu asta. (Cuvântul "direct" aici, ca de obicei în matematica modernă, înseamnă o linie infinită).
Modelul 2. Axiul paralel
Listele axiomelor lui Euclid în diferitele copii vechi suprapuse ale "Elementelor" diferă una de cealaltă - poate că nu toate axiomele (și postulatele) citate în ele aparțin Euclidului însuși. Cea mai comună este următoarea listă de axiome.
Aceleași sunt egale una cu cealaltă.
Și două linii nu conțin spațiu.
Întrebarea naturală care apare atunci când ne cunoaștem cu postulatele și axiomele lui Euclid este că postulatele diferă de axiome. În general, se pare că axiomele, spre deosebire de postulate, se referă la proprietăți foarte generale ale unor cantități de natură foarte diferită, incluzând, de exemplu, numere, nu doar obiecte geometrice. Cu toate acestea, axioma 9 contrazice această interpretare. Semnificația acestei axiome este că două segmente nu se pot converge în două puncte diferite - adică să limiteze o anumită figură a unei zone finite.

Fig. 1. A IX-a axiom al lui Euclid
Acum vom formula această axie după cum urmează: "După două puncte, nu mai trece mai mult de o linie dreaptă". Încercați să înțelegeți care este diferența dintre această axiomă și postulatul 1?
Postulatul 1 afirmă existența a cel puțin unui segment cu capete la două puncte date, iar axiomul 9 este acela că există cel mult un astfel de segment.
Un rol important este jucat de axioma 7. De fapt, vorbim despre ea este că dacă impunem o cifră la alta, astfel încât acestea se potrivesc, atunci aceste cifre vor fi egale. Euclid folosește întotdeauna cuvântul „egal“, în sensul egalității zonei, și anume spațiul. E. egal (lungime, volum, unghiuri, cantități). În sensul modern al cuvântului „egal“ așa cum este aplicat la figuri geometrice înseamnă exact „meci de la impunerea unor“: cifre egale diferă doar în locul (sau, mai degrabă, egalitatea înseamnă că există o mișcare care transformă o formă în alta, o mișcare a însemnat transformare care păstrează distanța ca dacă cifra era solidă și am putea să o mutăm). Deja matematica XVII-lea. ei au înțeles egalitatea tocmai în acest sens; GV Leibniz a introdus un termen special pentru această egalitate-congruență. Deci axiomul 7, în termeni moderni, înseamnă că cifrele egale (congruente) sunt egale. (În acest caz, desigur, cifrele cu dimensiuni egale nu trebuie să fie egale).
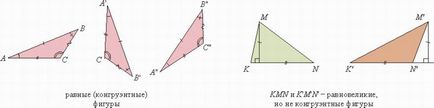
Fig. 2. Egalități egale și egale
Cu „aliniere“ Euclid demonstrează ceea ce se numește acum semnele egalității de triunghiuri, dar în viitor el evită aliniamente, invocând dovada egalitatea anumitor cifre cu privire la semnele deja dovedite ale egalității de triunghiuri.
În general, alegerea postulatelor și axiomelor în Euclid este de succes, dar sistemul său nu este complet: lipsesc multe axiome importante (de exemplu, cele stereometrice). Cu toate acestea, chiar Aristotel a crezut că uneori prezentarea acestei sau acelei științe este ignorată de anumite proprietăți și poziții datorită evidentității lor. Este posibil ca Euclid să nu-și stabilească scopul de a oferi o listă completă a declarațiilor necesare pentru dovezi suplimentare. Această problemă a părăsit matematicienii ulteriori.
Trimiteți-le prietenilor: