Să luăm în considerare ecuațiile omogene de conducere a căldurii.
În absența surselor externe de căldură. Punem problema Komi:
Găsiți o funcție U (x, t) care satisface ecuația:
Sensul fizic al problemei este determinarea temperaturii unei tije omogene infinite în orice moment prin cunoaștere. temperatura la momentul inițial t = 0.
Se crede că curenții. suprafața tijei este izolată termic (căldura de la tija nu dispare)
Să presupunem acum că funcțiile U (x, t) și funcțiile suficient de netede care scad cu
Atât de repede sunt acele creaturi. Convertește. Fourier
Transformarea Fourier a unei funcții cu privire la modificări. H.
2. Operațiunile diferențiale sunt legale.
Prin urmare, obținem transformările. Transformarea Fourier a celui de-al doilea derivat al funcției este legată de transformarea Fourier a funcției însăși. egalitate
Să aplicăm transformări. Fourier la ecuația inițială și începutul. Condiții. reducerea postului. problemă la problema Cauchy pentru ecuația diferențială obișnuită
Din prima ecuație există o ecuație:
Problema obținută este problema Komi pentru diferențele obișnuite. Eq.
Soluția acestei probleme este funcția
(care se verifică printr-o simplă substituire)
Arătăm funcția
este o transformare Fourier
Ie yavl. Convertește. Funcția Fourier a funcției:
Am dovedit funcția
Soluția poate fi scrisă ca:
După cum se știe, produsul a două transformări Fourier = transformarea convoluției. funcțiile este egală cu transformarea. Transformarea Fourier de la convoluția funcțiilor transformabile
Se obține o soluție a problemei inițiale Cauchy și denumirea. Formula lui Poisson pentru rezolvarea problemei Cauchy a ecuației de căldură.
Rămâne să se verifice dacă ecuația dată satisface condiția inițială, adică
Când găsim asta
Soluția găsită îndeplinește următoarea condiție:
Soluția fundamentală a ecuației de căldură (funcția Diran)
Formula Poisson care este în formula. fundamentală. soluție de ecuații conductivitate termică.
Considerând ca o funcție a argumentelor x, t, ea satisface ecuația căldurii
în care puteți verifica prin verificare.
Soluția fundamentală are un înțeles fizic important asociat cu conceptul de puls de căldură. Să presupunem în momentul inițial că distribuția inițială a temperaturii are forma:
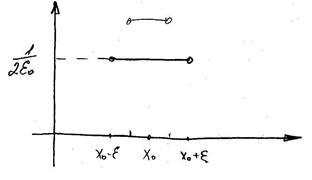
Cu cât este mai mare raftul
Apoi, în virtutea formulei lui Poisson, este distribuit. temperatura in tija este:
prin teorema valorii medii există un punct
. unde rezolvăm. apoi de la ultima egalitate pe care o obținem
- aceasta înseamnă că funcția reprezintă temperatura distribuită în tijă la un moment dat. dacă momentul inițial al momentului în punctul x0 are un vârf infinit de temperaturi și în alte puncte ale tijei temperatura este egală cu 0. O astfel de distribuție inițială a temperaturii poate fi aproximată. implementate după cum urmează:
În momentul până la punctul x0 al tijei, o flacără foarte îngustă, cu o temperatură foarte ridicată (pulsul de căldură), este ridicată pentru o perioadă foarte scurtă de timp - aceasta este descrierea distribuției inițiale a temperaturii. Formula Dirana este notată. Nu yavl. În sensul obișnuit, funcția este definită formal prin intermediul relațiilor
2. pentru orice interval. conține. punctul x0
Deci fundația. soluție yavl. soluția ecuației tijei cu distribuția inițială a temperaturii
Articole similare
Trimiteți-le prietenilor: