Funcția de două ori în mod continuu derivabile f (x) este o convexă (concavă), dacă și numai dacă funcția Hessian f (x) pentru x este pozitiv semidefinite (negativ) pentru orice x (a se vedea. Punctul de extremelor locale a funcției de multe variabile).
Punctele critice ale funcției:
- dacă Hessian este definit pozitiv, atunci x0 este un punct minim local al funcției f (x).
- Dacă Hessian este negativ definit, atunci x0 este punctul maxim local al funcției f (x).
- Dacă Hessianul nu este definit de semn (ia valori pozitive și negative) și este non-degenerat (), atunci x0 este punctul de șa a funcției f (x).
Criteriile pentru caracterul definitiv al matricei (teorema lui Sylvester)
O caracteristică pozitivă.- toate elementele diagonale ale matricei trebuie să fie pozitive;
- toți determinanții principali cheie trebuie să fie pozitivi.
- toate elementele diagonale nu sunt negative;
- toți factorii determinanți principali sunt non-negativi.
O matrice simetrică patrată de ordinul n. ale căror elemente sunt derivate parțiale ale funcției obiectiv secundare, se numește matrice hessiană și este desemnată prin:
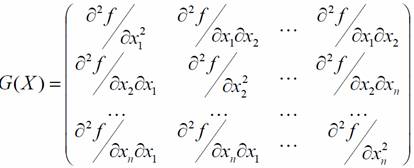
Pentru ca o matrice simetrică să fie pozitivă definită, este necesar și suficient ca toți minorii ei diagonali să fie pozitivi, adică,
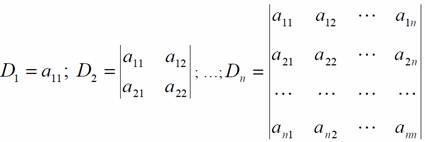
pentru matricea A = (aij) sunt pozitive.
Siguranță negativă.
Pentru ca o matrice simetrică să fie definitivă negativă, este necesar și suficient ca următoarele inegalități să fie:
(-1) k Dk> 0, k = 1. n.
Cu alte cuvinte, pentru ca forma patratică să fie definitivă negativă. este necesar și suficient ca semnele minorelor unghiului matricei formei patrate să fie alternate, începând cu semnul minus. De exemplu, pentru două variabile, D1 <0, D2> 0.
- Scădere în ordine. Variabilele sunt înlocuite. De exemplu, pentru o funcție a două variabile, aceasta este y = x. ca rezultat obținem o funcție a unei variabile x. În continuare, studiem comportamentul funcției pe liniile y = x și y = -x. Dacă în primul caz funcția la punctul studiat are un minim și în celălalt este un maxim (sau invers), atunci punctul de studiu este un punct de șa.
- Găsirea valorilor proprii ale lui Hessian. Dacă toate valorile sunt pozitive, funcția din punctul studiat are un minim, dacă toate valorile negative, există un maxim.
- O investigație a funcției f (x) într-o vecinătate a punctului ε. Variabilele x se înlocuiesc cu x0 + ε. Apoi, trebuie să dovedească faptul că funcția f (x0 + ε) dintr-un e variabilă, sau mai mare decât zero (atunci punctul x0 minim), sau mai mică decât zero (în cazul în care punctul x0 maxim).
Exemplul №1. Care dintre următoarele funcții este convexă sau concavă: f (x) = 8x1 2 + 4x1 x2 + 5x2 2.
Soluția. 1. Să găsim derivatele parțiale.
2. Rezolvăm sistemul de ecuații.
-4x1 + 4x2 + 2 = 0
4x1 -6x2 + 6 = 0
Avem:
a) Din prima ecuație exprimăm x1 și înlocuim în a doua ecuație:
x2 = x2 + 1/2
-2x2 + 8 = 0
De unde x2 = 4
Înlocuim aceste valori x2 în expresia pentru x1. Obținem: x1 = 9/2
Numărul de puncte critice este de 1.
M1 (9/2, 4)
3. Să găsim derivatele parțiale ale ordinii a doua.
4. Să calculam valoarea acestor derivate parțiale secundare la punctele critice M (x0; y0).
Calculam valorile pentru punctul M1 (9/2; 4)
Construim matricea hessiană:
D1 = a11 <0, D2 = 8> 0
Din moment ce minorii diagonali au semne diferite, nu se poate spune nimic despre convexitatea sau concavitatea funcției.
Exemplul 2. Determinați dacă funcția f (x) = 2x1 2 + x2 2 + sin (x1 + x2) este convexă în spațiul R2.
Soluția. O funcție de două ori diferențiată este convexă în spațiul R2. Dacă minorii principali unghiali ai matricei Hesse nu sunt negativi. Se scrie matricea hessiană - matricea derivatelor secundare:
Minorii unghiali sunt, respectiv, egali:
Astfel, D1> 0, D2> 0 pentru toate valorile, adică funcția f (x) este convexă.
Articole similare
Trimiteți-le prietenilor: