Numărul real este de asemenea definit ca o fracție zecimală infinită și apoi o expresie a formularului. unde există unul dintre simboluri sau. numit un semn al unui număr, este un număr întreg nonnegative, este o secvență de zecimale, adică elemente ale unui set de numere.
O zecime infinită este interpretată ca un număr care, pe o linie numerică, se află între punctele raționale ale formularului
Comparația numerelor reale sub formă de fracții zecimale infinite este realizată în mod biologic. De exemplu, puteți lăsa două numere nonnegative
În cazul în care. atunci; dacă asta. În cazul egalității, următoarea cifră este comparată. Și așa mai departe. În cazul în care. apoi după numărul finit de pași se va întâlni prima cifră. astfel încât. În cazul în care. atunci; dacă asta.
Cu toate acestea, atunci când se compară zecimalele infinite, vă rugăm să rețineți că numărul. În acest caz, în cazul în care înregistrarea unuia dintre numerele pe care le compara la început cu o anumită categorie, este o zecimală repetitivă, care se află într-o perioadă de 9, atunci ar trebui să fie înlocuit cu un post echivalent, cu zero în perioada.
Operațiile aritmetice asupra zecimalelor infinite sunt definite ca o continuare continuă [14] a operațiilor corespunzătoare pe numere raționale. De exemplu, suma numerelor reale este un număr real. îndeplinind următoarea condiție:
În mod similar, operația de multiplicare este definită pe setul de fracțiuni zecimale infinite.
În majoritatea cazurilor, coeficientul exact sub forma unei fracții zecimale nu poate fi obținut, indiferent cât de departe continuă diviziunea.
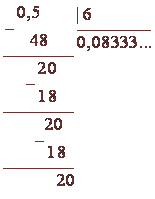
Fracțiunea este transformată într-o zecimală periodică pură, deoarece 27 nu este divizibilă nici de 2 sau 5. Fracțiunea este convertită într-o perioadă periodică mixtă, deoarece 12 este împărțită la 2.
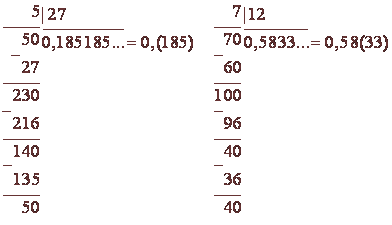
Dovedeste ca zecimea infinita 0.1234567891011121314. (după o virgulă, toate numerele naturale sunt scrise în ordine) este un număr irațional.
După cum se știe, numerele raționale sunt exprimate în fracții zecimale, care au o perioadă care începe cu un anumit semn. În urma acestui fapt, este suficient să se demonstreze că fracțiunea dată nu este periodică cu nici un semn. Să presupunem că nu este așa, iar o secvență T formată din n cifre este perioada fracțiunii, începând cu punctul zecimale. În acest caz, între cifrele după caracterul m-le există nenumărate, deci în secvența de cifre T există o cifră diferită de zero. Acest lucru înseamnă că, începând cu cifra m-a după punctul zecimal, există o cifră diferită de zero în orice n cifre dintr-un rând. Dar în notația zecimală a acestei fracții ar trebui să existe o notație zecimal a numărului 100. 0 = 10 k. unde k> m și k> n. Este clar că această înregistrare va fi găsită în partea dreaptă a cifrei m și conține mai mult de n zerouri la rând. Astfel, avem o contradicție care completează dovada.
Având în vedere o fracție zecimală infinită 0, a1 a2. Dovedeste ca numerele din notatia zecimala sa fie rearanjate astfel incat fractia rezultata sa exprime un numar rational.
O fracție exprimă un număr rațional dacă și numai dacă este periodic, începând cu un semn. Cifrele de la 0 la 9 sunt împărțite în două clase: în prima clasă includem acele figuri care apar în fracțiunea inițială un număr finit de ori, în clasa a doua - cele care apar în fracțiunea inițială infinit de multe ori. Începem să scriem o fracție periodică, care poate fi obținută din permutarea originală a cifrelor. Mai întâi, după zero și o virgulă, vom scrie într-o ordine arbitrară toate cifrele din prima clasă - fiecare de câte ori apare în înregistrarea fracțiunii originale. Cifrele înregistrate ale primei clase vor precede perioada din partea fracționată a fracțiunii zecimale. Apoi, într-o anumită ordine, vom scrie numerele din clasa a doua o dată. Combinația rezultată va fi numită o perioadă și o vom repeta de nenumărate ori. În acest fel, am scris fracțiunea periodică dorită, exprimând un număr rațional.
Dovada că în fiecare fracție zecimală infinită există o secvență de simboluri zecimale de lungime arbitrară, care în descompunerea fracțiunii are loc infinit de multe ori.
Fie m un număr întreg arbitrar pozitiv. Împărțim această zecimă infinită în segmente, cu m cifre în fiecare. Vor fi infinit multe astfel de segmente. Pe de altă parte, diferite sisteme constând în m cifre, există doar 10 m. adică un număr finit. Prin urmare, cel puțin unul dintre aceste sisteme trebuie repetat aici infinit de multe ori.
Notă. Pentru numere iraționale 2, p sau e, nici măcar nu știm ce număr se repetă infinit de multe ori în fracțiunile zecimale infinite care le reprezintă, deși fiecare dintre aceste numere, așa cum se poate arăta ușor, conține cel puțin două figuri diferite.
Verificați diviziunea de coloana respectivă
Astfel, toate numerele raționale sunt cuprinse între fracțiunile zecimale infinite ca zecimale periodice.
Numerele reale sunt zecimale infinite cu un semn plus sau minus, iar în cazul unei periodicități a unei fracții, un astfel de număr real este numit rațional, altfel este irațional.
Numărul a = 0.1010010001. ca o fracție zecimală infinită infinită este irațională.
Este relativ ușor de determinat în raportul egalității și ordinului ("mai mare"). Fie a = 0. 1. 2. b = 0. 1. 2
numere reale. Presupunem că ele sunt egale dacă sunt de același semn și k = 0, 1, 2. k = k.
Fie a, b să fie de același semn "+". Numărul a este mai mare decât numărul b (a b) dacă există k = 0, 1, 2. că i = i pentru i = 1, 2. k-1 și kk
Articole similare
Trimiteți-le prietenilor: