Lecție de "mișcare"

Scurtă descriere a documentului:

TEXTUL DE LECȚIUNE DECLARAȚIA:

Continuăm să ne cunoaștem mișcarea.

În ultima lecție, ați aflat despre un alt fel de mișcare - simetrie axială.

Îmi amintesc că simetria axială cu axa a este o cartografiere a spațiului pe ea însăși, sub care orice punct K trece peste punctul K1 simetric în jurul axei a.

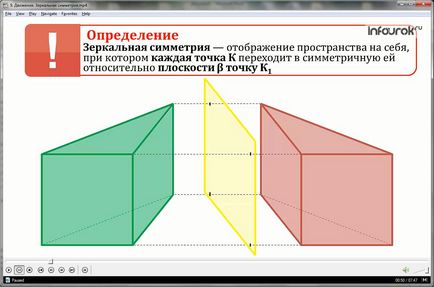
Maparea pe sine, în care fiecare punct K devine simetric față de punctul de un plan β s K1 numit oglindă simetrie (simetrie în raport cu planul β).

1. Introducem sistemul de coordonate cartezian (dreptunghiular) Oxyz astfel încât planul Oxy să coincidă cu planul de simetrie.

2. Să găsim conexiunea dintre punctele M (x; y; z) și M1 (x1; y1; z1), care sunt simetrice în raport cu planul Oxy. Dacă punctul M nu aparține unui plan dat, atunci planul Oxy:

a) trece prin mijlocul segmentului MM1;

b) este perpendicular pe segmentul MM1.

Din prima condiție, folosind formulele pentru coordonatele mijlocului segmentului, avem:

z + z1 = 0, unde z = -z1

Din a doua condiție rezultă că segmentul MM1 este paralel cu axa Oz. astfel, x = x1; y = y1.

Aceste formule sunt valabile și în cazul în care punctul M se află în planul Oxy.

3. Să considerăm două puncte: A - cu coordonatele (x1, y1, z1) și B - coordonatele (x2; y2; z2), și să dovedească faptul că distanța dintre punctele A1 și B1, că acestea sunt simetrice, egale cu AB.

Punctele A1 și B1 au coordonate

A1 (x1; y1; -z1) și B1 (x2; y2; -z2).

Prin formula distanțelor dintre două puncte, găsim:

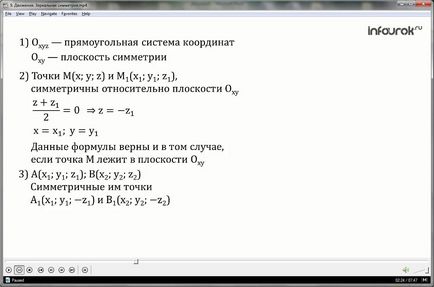
Evident, lungimea segmentului AB este egală cu lungimea segmentului A1B1, adică distanța dintre puncte este păstrată.

Astfel, am demonstrat că simetria oglindă este o mișcare.

Vom analiza mai multe probleme prin aplicarea cunoștințelor acumulate.

Dovedeste ca liniile a si a1 se afla in acelasi plan, daca, sub simetria oglinzii, linia a este mapata in linia a1.

1. Introducem planul de simetrie Oxy.

Să luăm în considerare două cazuri:

- linia dreaptă a este paralelă cu planul Oxy.

- Linia dreaptă a nu este paralelă cu planul Oxy.

În cazul planul Oxy drepte și paralele și au: punctele M și L, N și K sunt simetrice (Direct aparțin simetrice), apoi MA = AL, NB = BK.

În plus, toate aceste segmente sunt egale una cu cealaltă: MA = AL = NB = BK, deoarece planul Oxy este planul de simetrie.

Linile ML, NK sunt perpendiculare pe planul Oxy, astfel încât ML este paralel cu NK (două linii drepte perpendiculare pe plan sunt paralele unele cu altele).

Astfel, am obținut că MLKN quadrilateral este un dreptunghi.

Prin urmare, liniile LK și MN sunt paralele ca fețe opuse ale dreptunghiului MLKN. Aceasta înseamnă că liniile drepte a și al, pe care se află liniile paralele LK și MN, vor fi paralele și, prin urmare, se află în același plan.

După cum este necesar pentru a dovedi.

2. În cazul în care linia dreaptă a nu este paralelă cu planul Oxy, linia dreaptă a intersectează planul dat la punctul P.

Sub simetrie, punctul P intră în sine, deoarece se află în planul de simetrie Oxy.

Astfel, punctul P aparține liniei a1.

Am obținut că liniile a și a1 au un punct comun, de aceea se află în același plan.

După cum este necesar pentru a dovedi.

Astfel, am demonstrat că liniile a și a1 se află întotdeauna în același plan, dacă, sub simetrie oglindă, linia dreaptă a este mapată la linia a1.

Pentru simetria oglinzii față de planul α, planul β este mapat pe planul β1. Dovedeste ca daca planul β este paralel cu planul α, atunci planul β1 este de asemenea paralel cu planul α.

1. Alegeți trei puncte A, B, C în planul β care nu se află pe aceeași linie.

2. Construcție suplimentară: segmente de tragere AA2, BB2, CC2 perpendiculare pe planul α.

Noi extindem aceste segmente pentru punctele A1, B1, C1, astfel încât A2A1 = AA2, V2V1 = BB2, CC2 = S2S1.

Avem ca AA1V1V patrulater - un dreptunghi, ca AA1 și BB1 = AA1║VV1 (prin simetrie avioane p și p1).

3. Astfel, A1B1AB, BB1 = CC1 și BB1NCC1, atunci BB1C1C este un dreptunghi.

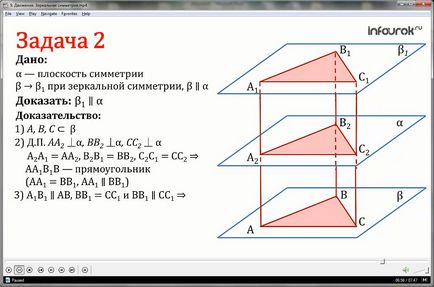
4. Planul β trece prin punctele A1, B1, C1 și acest plan este unic.

5. Este cunoscut faptul că, dacă liniile care se intersectează (BA și BC) a unui plan (β), paralele cu cele două linii care se intersectează (V1A1 și B1C1) ale celuilalt plan (β1), atunci aceste planuri sunt paralele.

Astfel, am demonstrat că planurile β și β1 sunt paralele.

Articole similare

• Lecție de geometrie în clasa a XI-a a profesorului de curente și

• Lecții și articole despre interfața solidă în tipuri și descrieri ale solidelor

• O lecție este un algoritm pentru rezolvarea ecuațiilor patratice

Trimiteți-le prietenilor: