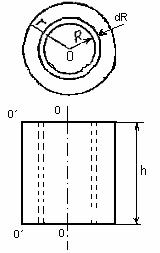
Fig. 28.1. Pentru a calcula momentul inerției cilindrului
Calculul integralului (28.4), și mai mult al integralității (28.3), este, în general, o problemă foarte complicată. Cazul este mult simplificat în cazul corpurilor aximetrice omogene. De exemplu, găsim momentul inerțiunii unui cilindru omogen în raport cu axa sa geometrică OO (Figura 28.1). Împărțim cilindrul în straturi de rază R și grosime dR. Greutatea acestui strat este:
unde (dV este volumul stratului).
Toate punctele din strat sunt separate de axa OO cu aceeași distanță R. Prin urmare, contribuția stratului la momentul inerției este
După integrarea acestei expresii în raport cu R în intervalul de la 0 la r (r este raza cilindrului), obținem momentul necesar de inerție:
(m = # 961; hpr 2 este masa cilindrului). Observăm că expresia obținută nu depinde de înălțimea cilindrului h. În consecință, formula (28.5) determină, de asemenea, momentul inerției discului subțire față de axa care trece prin centrul său perpendicular pe acesta.
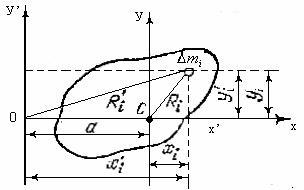
Fig. 28.2. Axele C și O sunt perpendiculare pe planul desenului. Axele x, y, x și y sunt de asemenea centrul masei C situate în planul desenului. Au următoarele relații: x'i = xi + a, y'i = yi
Luați în considerare un corp arbitrar și două axe paralele unul cu celălalt, dintre care una trece axa C prin centrul de masă al corpului, iar cealaltă axă 0 este o distanță de a de la prima (figura 28.2). Alegem axele de coordonate x, y și x ', y' așa cum se arată în figură.
Momentul de inerție I față de axa O este dat de
Împărțim această expresie în trei sume:
Prima sumă reprezintă momentul inerției Ic în raport cu axa care trece prin centrul de masă. Suma Σ # 8710; mi dă masa corporală m. În cele din urmă Σxi Mi = xc m, unde xc sunt coordonatele centrului de masă, care este egal cu zero pentru originea aleasă. Astfel ajungem la relație
Această relație exprimă teorema lui Steiner. care afirmă că momentul de inerție relativ la o axă arbitrară este egal cu suma momentului de inerție față de axa paralelă cu cea dată și care trece prin centrul de masă al corpului și produsul masei corpului pe pătrat al distanței dintre axe. Teorema lui Steiner reduce calculul momentului de inerție față de o axă arbitrară la calculul momentului de inerție în jurul axei care trece prin centrul de masă al corpului.
Utilizăm teorema lui Steiner pentru a găsi momentul inerției I 'al unui cilindru omogen cu privire la axa O'O, care coincide cu generatorul cilindrului (vezi Figura 28.1). În acest caz, Ic este determinat de expresia (28.5), distanța dintre axele a este egală cu raza cilindrului r. Prin urmare, conform (28.6)
Nu este dificil să se calculeze momentul inerției unei tije omogene subțiri cu masa m și lungime l față de axa OO perpendiculară pe ea, care trece prin capătul său (figura 28.3).
Fig. 28.3. Masa unui element de tijă cu lungimea dx este dm = (m / l) dx
Rețineți că tija poate fi considerată subțire dacă dimensiunea transversală maximă a tijei sale este mai mică decât lungimea l. Conform formulei (28.2)
Articole similare
-
Intercharmnet - portal de cosmetică și cosmetică pentru cosmetică și parfumerie,
-
Înainte de nunta poza de poveste de dragoste - nunta aici nunta
Trimiteți-le prietenilor: