Centrul forțelor paralele

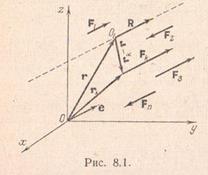
Presupunând că această condiție este îndeplinită, pentru a afla ce se întâmplă cu rezultanta în timpul linii simultane de rotație de date paralele de acțiune a forțelor pe unul și același unghi, atunci când punctul de aplicare al acestor forțe rămân neschimbate și apoi liniile de acțiune ale forțelor se produce în jurul unor axe paralele.

În aceste condiții sistemul forță rezultantă dată rotit simultan de același unghi, rotația are loc în jurul unui punct fix numit centrul de forțe paralele. Continuăm să demonstram această afirmație.

Să presupunem că pentru sistemul de forțe paralele luate în considerare vectorul principal nu este egal cu zero, prin urmare, acest sistem de forțe este redus la sistemul rezultat. Fie ca punctul să fie orice punct al liniei de acțiune a acestui rezultat. Fie acum vectorul de rază al punctului în raport cu polul ales. a este vectorul de rază al punctului de aplicare a forței.

Conform teoremei lui Varignon, suma momentelor tuturor forțelor sistemului față de punct este egală cu zero:

. (8.2), deoarece punctul se află pe linia de acțiune a rezultatului.

Ecuația rezultată poate fi rescrisă în următoarea formă:

Acum introducem un vector unic. paralel cu liniile de acțiune ale forțelor. Apoi orice forță poate fi reprezentată în formă

în cazul în care. Dacă direcția forței și a vectorului coincid și. dacă și sunt îndreptate opuse una față de cealaltă. Este evident că în acest caz

. (8.5) Înlocuim expresiile (8.4) și (8.5) în relația (8.3), obținem

Ultima egalitate este satisfăcută pentru orice direcție a forțelor (adică direcția vectorului unității) numai cu condiția ca primul factor să fie zero:

La rândul său, această ecuație are o soluție unică în raport cu vectorul de rază. care determină punctul de aplicare al rezultatului, care nu își schimbă poziția atunci când liniile de forță sunt rotite. Un astfel de punct este centrul forțelor paralele, ceea ce dovedește existența lui. Denumirea vectorului de rază al centrului forțelor paralele prin. din (8.7) obținem

Lasă-l să fie. . - coordonatele centrului forțelor paralele, a. . - coordonatele punctului de centru al aplicării forței arbitrare; atunci coordonatele punctului central al forțelor paralele pot fi găsite din formulele:

se numesc respectiv momentele statice ale unui sistem de forțe dat în raport cu planurile de coordonate. . .

Rețineți că dacă originea este aleasă în centrul forțelor paralele, atunci

iar momentele statice ale sistemului de forțe date sunt zero.

Corpul unei forme arbitrare, care se află în câmpul gravitațional, poate fi împărțit prin secțiuni paralele cu planurile de coordonate în volume elementare. Dacă vom neglija dimensiunea corpului, în comparație cu raza Pământului, forța de gravitație care acționează asupra fiecărui volum elementar, pot fi considerate paralele între ele. Indicăm prin volumul unui paralelipiped elementar cu centrul la un punct. și forța de gravitație care acționează asupra acestui element este prin intermediul. Apoi greutatea specifică medie a unui element de volum este un raport. Tragerea paralelipipedului într-un punct. obținem greutatea specifică la un anumit punct al corpului, ca limită a greutății specifice medii

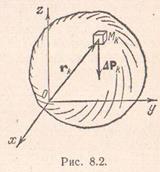
Formula (8.11) determină poziția unui punct.

Centrul de greutate este un punct care este punctul limită pentru. Cu alte cuvinte, centrul de greutate al unui corp este un punct al cărui vector de rază este definit de următoarea limită:

(8.12) sau, schimbând gravitatea specifică,

. (8.13) Cu o astfel de tranziție limitativă, se presupune că dimensiunile tuturor paralelipipedelor tind să fie zero. Limitele numitorului în formulele (8.12) și (8.13) sunt egale cu greutatea corporală

Deoarece limitele sumelor integrale din numărătorul și numitorul Formula (8.13) sunt definite integralele peste un volum al corpului, acesta poate fi reprezentat după cum urmează:

Coordonatele centrului de greutate sunt determinate de formulele:

Se spune că un corp este omogen dacă. În acest caz, cantitatea este luată în formulele (8.14) pentru semnele integralelor în numărător și numitor și este redusă. Denominații în formule (8.14) după reducerea lor la egal cu volumul corpului. Astfel, obținem

Centrul de greutate al unui corp omogen este adesea numit centrul de greutate al unui volum.

În unele cazuri, corpul poate fi considerat o placă sau coajă subțire.

Să găsim centrul de greutate al unei cochilii omogene, presupunând că greutatea unui element al suprafeței sale este proporțională cu aria acestui element

Și, prin urmare, greutatea corpului (este aria suprafeței luate în considerare).

Din definiția centrului de greutate în conformitate cu formulele (8.15), obținem pentru

Centrul de greutate al unei cochilii omogene se numește centrul de greutate al suprafeței.

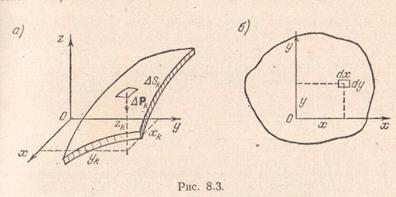
După cum rezultă din formulele (8.16), determinarea coordonatelor centrului de greutate al suprafeței este legată de calculul integralelor pe suprafață.

Pentru o placă plană omogenă, obținem

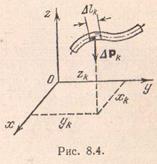
unde este lungimea tijei.

Valoarea se numește "greutate de funcționare". În această ipoteză, cantitatea este constantă. Apoi, în conformitate cu formulele (8.15), coordonatele centrului de greutate al tijei omogene au forma

Centrul de greutate al tijei curbe se numește centrul de greutate al liniei.

Articole similare

• Centrul de Sănătate Centrul de Sănătate - Prețuri și Feedback

• Centrul Științifico-Practic Republican de Traumatologie și Ortopedie din Belarus

• Intan, centre de implantare și stomatologie, o rețea de adrese

Trimiteți-le prietenilor: