În această lecție vom cunoaște conceptul de arccotangent. La începutul lecției, luăm în considerare graficul funcției y = ctg t pe intervalul [0; π] și proprietățile sale. În continuare, dăm definiția arccotangentului ca soluție a problemei inverse. Să luăm în considerare descoperirea arccotangentului pe cercul numeric și pe linia cotangentelor. Apoi luăm în considerare și demonstrăm proprietatea importantă a arccotangentului, îl ilustrăm pe grafic și rezolvăm câteva exemple. Și vom dovedi formula care leagă arctangent și arccotangent. La sfârșitul lecției, vom rezolva câteva exemple de găsire a unui arccotangent.
Subiect: Ecuații trigonometrice
Lecția: Arkkotangens și soluția ecuației ctgx = a
1. Graficul grafic al funcției y = ctgt, conceptul de arccotangent
Să analizăm în detaliu construirea graficului funcțional (figura 1).
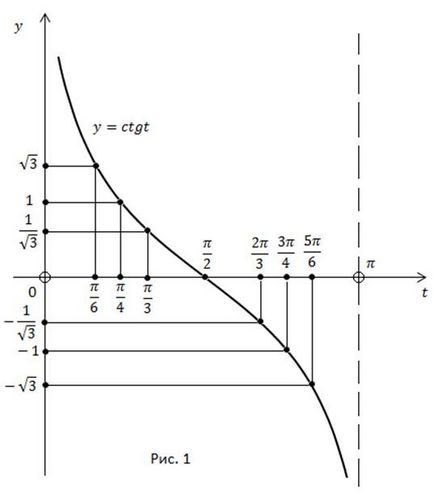
Funcția scade monotonic pe interval De asemenea, în acest interval, funcția își ia toate valorile de la
Problema inversă are o soluție unică. Valoarea funcției este dată - este obținută cu o singură valoare a argumentului pe interval.
2. Definiția arccotangentului
Arccotangența unui număr este un număr al cărui cotangent este
3. Arccotangent pe un cerc numeric
Luați în considerare arccotangentul pe cercul trigonometric (Figura 2).
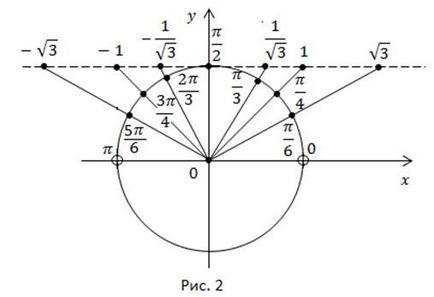
Exemplu: Găsiți în cerc trigonometric următoarele valori: În ce măsură este valoarea
4. Rezolvarea problemelor
Să ilustrăm proprietatea importantă a arccotangentului.
Fie Arccotangentul egal dacă argumentul este egal cu Arccotangent este egal cu atunci când argumentul este egal (Figura 3).
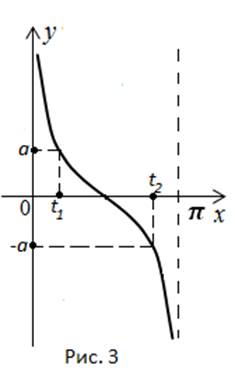
Pe grafic, vedem asta
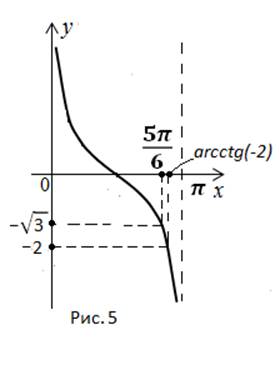
Să ilustrăm soluția pe grafic (figura 4).
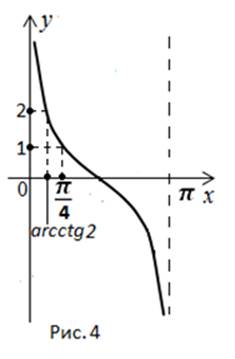
Să justificăm răspunsul. Comparați argumentele: Dar funcția scade pe interval Prin urmare, la o valoare mai mică a argumentului există o valoare mai mare a funcției u
b) Estimați numărul de
Problema 2. Pentru a verifica pe exemple specifice identitatea:
Problema 3. Calculați
Problema 4. Calculați
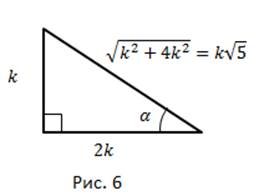
Il ilustram solutia pe un triunghi drept.
Având în vedere un unghi Să desemnați catehetul contiguat drept piciorul opus (figura 6). Prin teorema pitagoreană, hypotenuse este
Problema 5. Calculați
5. Concluzie, concluzie
Am aflat ce arccotangent este. În următoarea lecție vom rezolva cu ea ecuația pentru orice
21,32, 21,36, 21,48 (b, c).
2. Problemele portalului de Internet. ru.
3. Portalul educațional pentru pregătirea examenelor.
Se încarcă.
Se încarcă.
Lucrări populare
- Peisaje în versurile lui Alexander Puskin
- O analiză a poeziei de către A. Blok "Pe câmpul Kulikovo"
- Tată și fiu în povestea lui D. Aldridge "The Last Inch"
- Viața și munca Goethe V. Și
- Deciziile instanței de arbitraj. sarcini
- Proiectarea unei întreprinderi de catering public Proiectarea unui snack bar. partea 2
- A. S. Pushkin și S.A. Yesenin despre natura rusă
-
Statistici privind proiectele
Articole similare
Trimiteți-le prietenilor: