Vectori în spațiul tridimensional
Reprezentarea geometrică a vectorului este un segment direcționat al unei linii drepte, care este prezentat în Fig. 1. Fiecare vector are două proprietăți: lungimea (numită și modulul sau norma vectorului) și direcția. Din acest motiv, vectorii sunt foarte convenabili pentru modelarea cantităților fizice, caracterizate prin modul și direcția. De exemplu, în capitolul 14, implementăm un sistem de particule. Procedând astfel, vom folosi vectori pentru a simula viteza și accelerația particulelor noastre. Pe de altă parte, în grafica 3D a computerelor, vectorii sunt adesea utilizați numai pentru direcțiile de modelare. De exemplu, de multe ori, trebuie să specificăm direcția propagării razelor de lumină, orientarea feței sau direcția camerei, care privește lumea tridimensională. Vectorii oferă un mecanism convenabil pentru specificarea direcției în spațiul tridimensional.
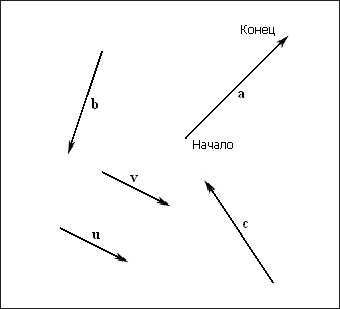
Fig. 1. Vectori liberi definiți independent de sistemul de coordonate
Deoarece locația nu este o caracteristică a unui vector, doi vectori de aceeași lungime și orientați în aceeași direcție sunt considerați egali, chiar dacă sunt localizați în diferite locuri. Rețineți că doi astfel de vectori vor fi paralele unul cu altul. De exemplu, în Fig. 1 vectorii u și v sunt egali.
În Fig. 1 se poate observa că discuția vectorilor poate fi efectuată fără a menționa sistemul de coordonate, deoarece toate informațiile relevante, - lungimea și direcția, - vectorul conține în sine. Adăugarea unui sistem de coordonate nu adaugă informații vectorului; mai degrabă, se poate spune că un vector ale cărui valori sunt parte integrantă este pur și simplu descris cu privire la un anumit sistem de coordonate. Și dacă schimbăm sistemul de coordonate, vom descrie doar același vector în raport cu celălalt sistem.
Luând notă de acest punct important, ne îndreptăm spre studiul modului în care vectorii sunt descriși în sistemul tridimensional de coordonate carteziene la stânga. În Fig. 2 prezintă sistemele de coordonate din stânga și dreapta. Diferența dintre acestea este direcția pozitivă a axei Z. În sistemul de coordonate din stânga, direcția pozitivă a axei Z este imersată în pagină. În sistemul de coordonate din dreapta, direcția Z pozitivă este îndreptată din pagină.
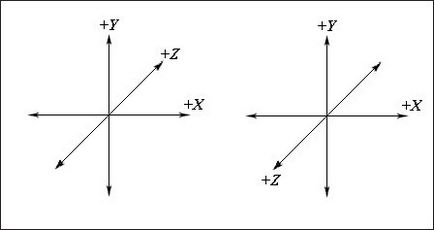
Fig. 2. Stânga este sistemul de coordonate la stânga. Rețineți că direcția pozitivă a axei Z este direcționată adânc în pagină. Sistemul de coordonate din dreapta este afișat la dreapta. Aici direcția pozitivă a axei Z este direcționată din pagină
Deoarece locația vectorului nu-și schimbă proprietățile, putem transfera vectorii astfel încât începutul fiecăruia să coincidă cu originea coordonatelor sistemului de coordonate selectat. Când originea vectorului coincide cu originea, se spune că vectorul este în poziția standard. Astfel, dacă vectorul este într-o poziție standard, îl putem descrie specificând doar coordonatele punctului final. Vom numi aceste coordonate componentele vectorului. În Fig. 3 prezintă vectorii prezentați în Fig. 1, care au fost mutate în poziții standard.
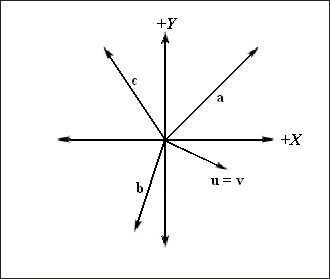
Fig. 3. Vectori în poziția standard definită în sistemul de coordonate specificat. Rețineți că vectorii u și v coincid complet între ei deoarece sunt egali
Deoarece descriem un vector în poziția standard, indicând punctul său final, ca și cum am descrie un singur punct, este ușor să confundăm punctul și vectorul. Pentru a sublinia diferențele dintre aceste două concepte, le dăm din nou definiția fiecăruia. Punctul descrie numai locația în sistemul de coordonate, în timp ce vectorul descrie magnitudinea și direcția.
Vom folosi litere aldine pentru a desemna vectori, dar uneori vom folosi litere mari albe. Iată un exemplu de vectori cu doi, trei și patru dimensiuni, respectiv: u = (ux. Uy), N = (Nx, Ny, Nz), c = (cx.
Acum introducem patru vectori tridimensionali specifici, care sunt arătați în Fig. 4. Primul dintre acestea se numește vectorul zero. iar valorile tuturor componentelor sale sunt zero; vom desemna un astfel de vector in boldface cu zero: 0 = (0, 0, 0). Următorii trei vectori specifici se numesc vectori de bază (vectori de bază) ai sistemului tridimensional de coordonate. Aceste vectori, direcționați de-a lungul axelor X, Y și Z ale sistemului nostru de coordonate, vom apela i. j și k, respectiv. Modulul acestor vectori este unul și definiția arată astfel: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
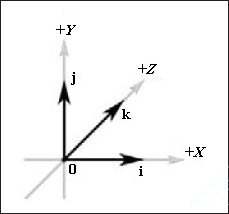
Fig. 4. Vectorii zero și vectorii de bază ai sistemului tridimensional de coordonate
Un vector a cărui lungime este egală cu una se numește vectorul unitate sau vectorul unității.
În biblioteca D3DX, putem folosi clasa D3DXVECTOR3 pentru a reprezenta vectori în spațiul tridimensional. Definiția sa este după cum urmează:
Rețineți că D3DXVECTOR3 moștenește componente din D3DVECTOR. a cărui definiție este după cum urmează:
La fel ca și cantitățile scalare, vectorii au propriile aritmetice, ceea ce este evident din prezența descrierilor de operații matematice în definiția clasei D3DXVECTOR3. Poate că acum nu știți ce fac aceste metode. În următoarele subsecțiuni vom lua în considerare aceste operații cu vectori, alte funcții auxiliare pentru lucrul cu vectori din biblioteca D3DX și câteva caracteristici importante ale procesării vectoriale.
Deși interesul principal pentru noi sunt vectori în spațiul tridimensional, în timp ce angajăm în programarea 3D, vom întâlni uneori vectori în spații bidimensionale și patru-dimensionale. Biblioteca D3DX oferă clasele D3DXVECTOR2 și D3DXVECTOR4. destinate reprezentării vectorilor în spații bidimensionale și respectiv în patru dimensiuni. Vectorii în spații cu un număr diferit de dimensiuni au aceleași proprietăți ca și vectorii în spațiul tridimensional, și anume, lungimea și direcția, numai numărul de măsurători diferă. În plus, operațiile matematice cu vectori, cu excepția produsului vectorial (vezi secțiunea "Produs vector", mai târziu în acest capitol), care este definită doar pentru un sistem tridimensional de coordonate, pot fi generalizate pentru vectori de orice dimensiune. Astfel, cu excepția produsului vectorial, toate operațiile pe care le discutăm pentru vectori în spațiu tridimensional sunt extinse la vectori în spații bidimensionale, patrudimensionale și chiar n-dimensionale.
Egalitatea vectorilor
În geometrie, doi vectori sunt considerați egali dacă direcționează în aceeași direcție și au aceeași lungime. În algebră, ei spun că vectorii sunt egali dacă au același număr de dimensiuni și componentele lor corespondente sunt egale. De exemplu, (ux.Uy.Uz) = (vx.Vy.Zv) dacă ux = vx. uy = vy și uz = vz.
În cod, putem verifica dacă doi vectori sunt egali, folosind operatorul de egalitate supraîncărcat:
În mod similar, putem verifica dacă cei doi vectori nu sunt egali utilizând operatorul de inegalitate supraîncărcat:
Compararea numerelor cu puncte în virgulă mobilă ar trebui să fie foarte precisă, deoarece din cauza erorilor de rotunjire, două numere de puncte în virgulă care trebuie să fie egale pot varia ușor. Din acest motiv, verificăm egalitatea aproximativă a numerelor în virgulă mobilă. Pentru aceasta, am determinat EPSILON-ul constant. conținând o valoare foarte mică care va servi drept "tampon". Vom spune că două numere sunt aproximativ egale dacă diferența dintre ele este mai mică decât EPSILON. Cu alte cuvinte, EPSILON ne dă un fel de toleranță pentru erorile de rotunjire în cifrele cu virgulă mobilă. Următoarea funcție arată modul în care EPSILON poate fi folosit pentru a verifica egalitatea a două numere cu puncte în virgulă mobilă: Nu vă faceți griji despre acest lucru prin lucrul cu clasa D3DXVECTOR. deoarece operațiile de comparație supraîncărcate vor face totul pentru noi, dar este foarte important să știm despre această caracteristică a comparării numerelor cu puncte în virgulă mobilă.
Calculul modulului unui vector
În geometrie, modulul unui vector este lungimea unui segment al liniei direcționate. În algebra, cunoscând componentele vectorului, putem calcula modulul său prin următoarea formulă:
Linii verticale în | u | Indicați modulul u.
În codul pentru scăderea a doi vectori, vom aplica un operator de supracurent suprasolicitat:
Așa cum se poate vedea în fig. 6, operația de scădere a vectorului returnează un vector al cărui început coincide cu sfârșitul vectorului v. și sfârșitul cu sfârșitul vectorului u. Dacă interpretăm componentele u și v drept coordonate ale punctelor, rezultatul scăderii este un vector direcționat de la un punct la altul. Aceasta este o operație foarte convenabilă, pentru că adesea trebuie să găsim un vector care să descrie direcția de la un punct la altul.
Înmulțirea unui vector cu un scalar
După cum se poate observa din titlul secțiunii, putem multiplica un vector cu un scalar, ca urmare a faptului că vectorul este scalat. Dacă factorul de scalare este pozitiv, direcția vectorului nu se modifică. Dacă factorul este negativ, atunci direcția vectorului se schimbă spre invers (inversat).
Clasa D3DXVECTOR3 oferă operatorului înmulțirea unui vector cu un scalar:
Produs scalar al vectorilor
Produsul scalar al vectorilor este prima dintre operațiile de multiplicare definite în algebra vectorială. Acest produs se calculează după cum urmează:
Formula de mai sus nu are o interpretare geometrică evidentă. Folosind teorema cosinus 1. obtinem relatia u v v | | u || v | cos j. care spune că produsul scalar al a doi vectori este egal cu produsul cosinus al unghiului dintre vectori și moduli vectorilor. Deci, dacă u și v sunt vectori unici, produsul lor scalar este egal cu cosinusul unghiului dintre ele.
Iată câteva proprietăți utile ale unui produs scalar:
- Dacă u v v = 0, atunci u ^ v.
- Dacă u v v> 0, atunci unghiul j între două vectori este mai mic de 90 de grade.
- Dacă u v v <0, значит угол j между двумя векторами больше 90 градусов.
Simbolul ^ denotă "ortogonal" sau (care este același lucru) "perpendicular".
Pentru a calcula produsul scalar al a doi vectori în biblioteca D3DX, următoarea funcție este destinată:
Produs vector
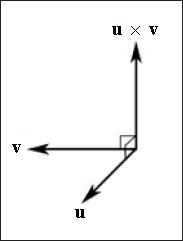
A doua formă a operației de multiplicare definită în algebra vectorială este produsul vectorial. Spre deosebire de un produs scalar, rezultatul căruia este un număr, rezultatul produsului vectorial este un vector. Produsul vectorial al doi vectori u și v este un alt vector, p. care este reciproc perpendiculară pe vectorii u și v. Aceasta înseamnă că vectorul p este perpendicular pe vectorul u și simultan vectorul p este perpendicular pe vectorul v.
Produsul vector este calculat folosind următoarea formulă:
În forma componentă, calculul arată astfel:
Se calculează j = k × i = (0, 0, 1) x (1, 0, 0) pentru a verifica dacă vectorul j este perpendiculară atât pe vectorul i. și vectorul k.
Astfel, j = (0, 1, 0). Rețineți că în secțiunea anterioară "Produs scalar al vectorilor" sa spus că dacă u v v = 0, atunci u ^ v. Deoarece j k k = 0 și j i i = 0, știm că vectorul j este perpendicular pe vectorul k. și vectorul i.
Pentru a calcula produsul vectorial al doi vectori în biblioteca D3DX, se intenționează următoarea funcție:
Este clar din Fig. 7, vectorul -p este, de asemenea, reciproc perpendicular cu vectorii u și v. Care dintre vectori, p sau -p va fi returnat ca rezultat al produsului vectorial este determinat de ordinea operanzilor. Cu alte cuvinte, u × v = - (v × u). Aceasta înseamnă că funcționarea unui produs vectorial nu este comutativă. Determinați ce vector va fi returnat ca rezultat, puteți utiliza regula stânga. (Noi folosim regula mâna stângă, din moment ce lucreaza cu sistemul stangaci de coordonate dacă am avea un dreptaci sistem de coordonate, ar trebui să utilizeze regula din dreapta ..) Dacă puneți degetele de la mâna stângă de-a lungul primului vector și palma mâinii - de-a lungul a doua, îndoit la 90 grade, degetul mare va indica direcția vectorului rezultat.
1 Teorema cosinusului determină relația dintre laturi și unghiurile triunghiului. Acesta prevede că, în orice triunghi lungime laterală pătrat egal cu suma pătratelor celorlalte două părți, fără a dubla produsul dintre lungimile laturilor cosinusul unghiului dintre ele. Dacă unghiul este drept, atunci teorema cosinusului devine teorema lui Pythagorean. cosinusul unghiului drept este 0.
Articole similare
Trimiteți-le prietenilor: