Dacă hiperbolă coincide cu jumătatea axelor reale și imaginare, adică a = b, atunci unghiul dintre asimptote este 2arctg (b / a) = 2arctg1 = π / 2, adică este direct. O astfel de hiperbolă se numește echilateral. Pentru ea, în afară de sistemul de coordonate canonice, în care axele coordonatelor coincid cu axele de simetrie ale hiperboliei, se mai ia în considerare și altul, ale cărui axe sunt asimptote. Obținem ecuația hiperbola în acest sistem de coordonate, pe care o denotăm prin Oxy. Să i, i să fie cadrul ei. și i ', j' este cadrul sistemului de coordonate canonice Ox'y '(Figura 8.1).
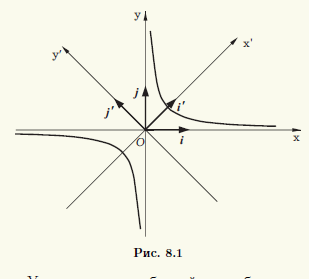
Sistemul de coordonate canonice se rotește relativ la sistemul Oxy cu un unghi de π / 4. Prin urmare, coordonatele x ', y' ale sistemului de coordonate canonice sunt exprimate prin coordonatele x, y (2) cu aceiași coeficienți: x '= √2 / 2x + √2 / 2y, y' = -√2 / 2x + √2 / 2y
Ecuația unei hiperbolări echilaterale în sistemul de coordonate canonice are forma (x ') 2 - (y') 2 = a 2. unde a este semi-axa reală (imaginară) a hiperbolei. Înlocuind variabilele canonice cu x, y în această ecuație, obținem 1/2 (x + y) 2 - 1/2 (x - y) 2 = a 2 sau
Ecuația (8.1) este numită ecuația hiperbola în asimptote.
Observație 8.1. Ecuația xy = -a 2/2 definește hiperbola conjugată pentru hiperbola esteoscel (8.1).
Exemplul 8.1. Gasim coordonatele punctelor vertexelor, focarelor si asimptotelor pentru hyperbola xy = -8 si o construim.
Această ecuație este o ecuație în asimptote pentru hiperbola esteoscelul conjugat. Prin urmare, axele de coordonate, i. Linile x = 0, y = 0, sunt asimptotele sale. Pentru această hiperbolă, -a 2/2 = -8, deci a 2 = 16 și a = b = 4. Dar atunci c = √ (a 2 + b 2) = √ (4 2 + 4 2) = 4√2, și luând în considerare notația de noduri și focare, găsim: A (-2√2; 2√2); B (2√2; -2√2); F1 (-4; 4); F2 (4; vezi figura 8.2).
Curbe de ordinul II - II
Trimiteți-le prietenilor: