Aceasta este, de asemenea, soluția X * este, de asemenea, optimă.
Teorema 1 indică principiul rezolvării problemelor LP: în loc să studieze un set infinit de soluții admisibile, este necesar să se investigheze un număr finit de puncte de colț.
1.3. Metodă grafică pentru rezolvarea problemei LP cu două variabile
Problema LP cu două variabile este dată
Metoda grafică de rezolvare se bazează pe posibilitatea reprezentării grafice a problemei SDE și găsirea soluției optime în ea.
1. ODR-ul problemei este construit ca intersecția domeniilor de soluții ale fiecăreia dintre constrângerile date. SDR poate fi un poligon convex; un domeniu convex poligonal nelimitat; zona goală; grindă; segment; singurul punct. Dacă SDT este un set gol, problema nu are o soluție pentru tipul de inconsecvență al sistemului de constrângeri.
2. Dacă SDR este neprinsă, determinați direcția de creștere a funcției obiectivului Z (X).
Pentru o valoare fixă arbitrară, ecuația definește pe plan o linie care este linia nivelului funcției obiectiv - linia pe care funcția obiectiv a problemei presupune o valoare constantă. Forma generală a ecuației liniei de nivel: c1x1 + c2x2 = l, l = const. Toate liniile de nivel sunt paralele între ele. Normal. Direcția este direcția de creștere a lui Z (X).
Astfel, la a doua etapă, sunt construite normalele liniilor de nivel și una dintre liniile de nivel (având puncte comune cu SDT).
3. Linia de nivel este deplasată în paralel în direcția normală a sarcinii la maximum, în direcția opusă în sarcină la minim. La un moment dat, aceasta va lua poziția limită: 1) va avea cel puțin un punct comun cu SDR; 2) SDR va fi într-un plan semi-plan cu privire la linia de nivel. Această linie de nivel este numită linia de referință. PDE-ul oricărei probleme LP are cel mult două linii de sprijin, dintre care unul poate avea o soluție optimă.
4. Dacă, în timp ce deplasăm linia de nivel de-a lungul SDT în direcția corespunzătoare, linia de nivel ajunge la infinit, atunci problema nu are o soluție optimă, având în vedere caracterul neobișnuit al funcției obiectiv. Scrieți Z (X) →.
5. Dacă problema are o soluție optimă, pentru ao găsi, este necesar să rezolvăm împreună ecuațiile liniilor care legau ODR și să aibă puncte comune cu linia de sprijin.
6. Calculați valoarea funcției obiectiv pe soluția optimă.
În funcție de tipul SDT și funcția obiectivă Z (X), problema LP poate avea o soluție unică, un set infinit de soluții și nu are o soluție optimă (vezi figurile 1, 2 și 3).
În figura 1, linia de nivel devine de două ori suportul în raport cu poligonul soluțiilor. Valoarea minimă a Z (X) este atinsă în t. A, valoarea maximă în T.
În figura 2, linia de susținere coincide cu una din laturile poligonului de decizie. Soluția optimă este orice combinație liniară convexă de puncte ale segmentului AE.
În Figura 3, SDR nu este limitat în direcția creșterii valorilor lui Z (X).
Exemplu 1. Să rezolvăm grafic problema LP:
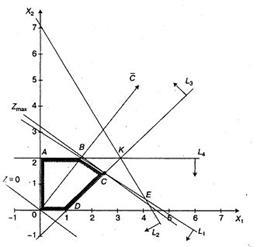
Construim un poligon al soluțiilor (figura 4). Pentru a face acest lucru, în sistemul de coordonate X10X2 din plan, reprezentăm liniile de graniță:
3x1 + 2x2 = 13 (L2);
Luând punct, de exemplu, originea coordonatelor, stabilim ce jumătate de plan determină inegalitatea corespunzătoare. Semiplanele, determinate de inegalități, sunt arătate în fig.4 prin săgeți. Domeniul soluțiilor este poligonul OABCD.
Construim o linie de nivel Z = 3x1 + 4x2 = 0 și un vector de gradient. Linia Z = 0 este deplasată paralel cu ea în direcția vectorului. Rezultă din figura 4 că, în ceea ce privește poligonul soluțiilor suportului, această linie devine în punctul C. unde funcția ia valoarea maximă.
Punctul C se află pe intersecția liniilor L1 și L3. Pentru a determina coordonatele sale, rezolvam sistemul de ecuatii:
Planul optim pentru problema este x1 = 2.4; x2 = 1,4. Înlocuind valorile x1 și x2 într-o funcție liniară, obținem:
.
1.4. Soluția problemelor de programare liniară prin metoda simplex
Reducerea problemelor LP la forma canonică
Dacă se prezintă modelul matematic al problemei LP:
atunci ei spun că problema este prezentată în formă canonică pentru un minim (maxim).
O înregistrare mai compactă:
(1) și (2) sunt intrări de coordonate ale problemei LP canonice.
Înregistrarea vectorială a problemei canonice:
Intrarea matrice a problemei canonice:
Orice problemă LP poate fi redusă la una canonică conform următoarelor reguli.
1. Trecerea de la problemă la max la problema la min (și invers) se realizează prin schimbarea semnului funcției obiectiv
Problemele inițiale și obținute au aceeași soluție optimă X *, iar valorile funcțiilor obiective pe această soluție diferă doar în semn.
2. Dacă există inegalități între constrângeri, atunci prin introducerea unor variabile non-negative suplimentare, ele sunt transformate în egalități
În funcția obiectivă, se introduc variabile suplimentare cu coeficienți zero, în acest caz nu afectează valoarea lui Z (X)
3. Dacă o anumită variabilă xk nu are constrângeri semnale, atunci ea este înlocuită (în funcția obiectivă și în toate constrângerile) de diferența dintre două noi variabile non-negative :, unde.
Exemplul 1. Reducem problema LP la forma canonică (cel puțin):
1. Trecem la problema minimului
2. Introducem în fiecare restricție a sistemului de constrângere variabilele de aliniere x 4, x 5, x 6. Sistemul este scris sub formă de egalități.
.
3. În forma canonică de înregistrare a problemelor LP, toate variabilele incluse în sistemul constrângerilor trebuie să fie negative. Să presupunem că, unde.
Înlocuind această expresie în sistemul constrângerilor și funcția obiectivă și scriind variabilele în ordinea creșterii indexului, obținem problema LP, reprezentată în forma canonică:
Principiul funcționării metodei simplex
Soluționarea problemelor LP pe baza metodei simplex constă într-o căutare direcționată a punctelor de colț ale SDT în direcția îmbunătățirii valorii funcției obiectiv.
Mai întâi, există o soluție fezabilă care corespunde unuia dintre punctele de colț ale SDT. Verificat adiacente punctelor sale unghiulare, care se află pe aceeași graniță SDT ca punct de colt curent (pentru o SDT bidimensional - pe aceeași parte a unui poligon, pentru un tridimensional - pe aceeași margine a poliedrului, etc ...).
Se poate dovedi că trecerea de la un punct de colț al SDT la alta (adiacentă) corespunde înlocuirii unei variabile în bază. O astfel de înlocuire înseamnă că una dintre variabilele non-ambigue (având o valoare zero) este inclusă în bază, adică crește, iar una dintre variabilele de bază scade la zero, adică este exclusă din bază. Alegerea acestor variabile se realizează în conformitate cu anumite reguli care asigură cea mai rapidă îmbunătățire a funcției obiective.
Dacă valoarea funcției obiectiv nu se îmbunătățește la nici unul dintre punctele de colț adiacente, atunci soluția problemei este finalizată; actualul punct de colț al SDE corespunde soluției optime a problemei. Dacă există puncte adiacente ODR unghiulare pentru care valoarea funcției obiectiv este îmbunătățită, atunci se face o tranziție la cea pentru care se obține cea mai rapidă îmbunătățire a valorii funcției obiectiv. Procesul se repetă pentru noul punct de colț al SDT. Căutarea punctelor de colț are loc până când se găsește o soluție optimă, adică până la atingerea punctului de colț al SDT, pentru care valoarea funcției obiectiv nu se îmbunătățește la nici unul dintre punctele adiacente.
Metoda se numește simplex, având în vedere că domeniile soluțiilor admisibile de probleme care au fost luate în considerare la etapa inițială a dezvoltării metodei au avut forma cea mai simplă (Figura 1):
1. Problema este redusă la forma canonică.
2.Tabelul inițial simplex este construit și soluția inițială fezabilă (punctul inițial de colț) este determinată.
3. Efectuați transformări de tabel simplex care corespund căutării punctelor de colț ale SDT, până când se obține o soluție optimă.
Luați în considerare implementarea acestui algoritm în rezolvarea problemei de programare liniară:
1. Rescriim problema în formă canonică, adăugând necunoscute suplimentare:
2. Scriem prima tabel simplu:
Dacă în ultimul rând nu există coeficienți negativi (printre numerele -c1, ... -c2), atunci soluția de bază (atunci când necunoscutele libere x1 = ... = xn = 0) vor fi optime. Într-adevăr, dacă vom crește de la 0 la cel puțin una dintre necunoscutele libere, atunci funcția va scădea.
Să presupunem, de exemplu, că -c1 <0, тогда, увеличивая число х1 будем получать большие значения функции. Если число a11>0, atunci dacă toate rămase necunoscute rămase x1 sunt egale, x1 poate fi mărită la cel mult b1 / a11. Dacă a11 0, atunci inegalitatea nu impune restricții asupra creșterii numărului x1 (atunci x1 poate fi mărită cât de mult se dorește). Prin urmare, dacă toți coeficienții a11, ..., ak1 sunt nepozitivi, atunci x1 poate crește fără restricții și, în plus, funcția va crește, de asemenea, nelimitat. În acest caz, nu există o soluție optimă.
3. Ne limităm la cazurile în care în prima coloană dintre numerele a11, ..., ak1 există coeficienți pozitivi: atunci numărul x1 poate fi mărit la valoarea x0 = min. Să se atingă un rând la rând și să lăsăm i1 = 1. Trecem la bază, luând x1 la bază în loc de xn + 1. Obținem un nou tabel simplex pentru care valoarea funcției crește cu un număr dx> 0.
Pentru un nou tabel simplex, în cazul în care ultima linie nu este coeficienți negativi soluție de bază corespunzătoare este optimă (funcția este de forma, în cazul în care numerele, ..., 0, și, prin urmare, crește numărul de x1, ..., xn + 1 este neprofitabilă). Dacă ultima linie are un coeficient negativ, atunci efectuăm din nou procedura precedentă (la trecerea la noua tabelă simplex). Într-un număr limitat de pași, obținem o soluție optimă de bază sau dovedim că nu există o soluție optimă.
Exemplul 2. Pentru executarea lucrărilor de fabricare a produselor de tip 1 și 2 există 10 unități din prima materie primă și 8 unități din materia primă II. Fiecare element de tip 1 consumă 2 unități din fiecare materie primă și pentru fiecare produs din cel de-al doilea tip se consumă 4 și 1 unitate de materie primă de fiecare tip. Planificați producția astfel încât numărul total de produse să fie cel mai mare.
Fie ca produsele de tip 1 și 2 să fie produse de unități x1 și x2, atunci materiile prime de tipul 1 vor fi consumate, iar materiile prime din al doilea tip. Este necesar să se găsească valoarea maximă a funcției pentru valori întregi non-negative ale argumentului.
Introducem necunoscutele auxiliare x3 și x4 (resturile de materii prime de tip 1 și 2) și obținem problema canonică:
Noi compunem tabela simplă originală:
Articole similare
-
Lecția # 1 - ghid de studiu, boli interne ale câinilor, pisicilor, păsărilor de curte
-
Scule de învatamânt de casă pentru școală, mâini cu pricepere, cărți
Trimiteți-le prietenilor: