Imaginația elipsei Wikipedia

Definiție [ ]

Elipsa este locusul punctelor M ale avionului euclidian. pentru care suma distanțelor față de două puncte date F 1> și F 2> (numite foci) este constantă și mai mare decât distanța dintre focare, adică

Definiții înrudite [ ]

• Trecând prin focurile elipsei, segmentul AB, ale cărui capete se află pe o elipsă, se numește axa majoră a acestei elipse. Lungimea axei principale este de 2 a în ecuația de mai sus.
• Un segment de CD perpendicular pe axa majoră a elipsei, care trece prin punctul central al axei principale, ale cărui capete se află pe o elipsă, se numește axa minoră a elipsei.
• Punctul de intersecție al axelor mari și mici ale elipsei se numește centrul său.
• Segmente, realizate din centrul elipsei la nodurile la axele majore și minore sunt numite, respectiv, axa principală și axa minoră a elipsei, și sunt desemnate a și b.
• Distanțele r 1> și r 2> de la fiecare dintre focare până la un punct dat pe elipsă sunt numite radii focale în acest punct.
• Distanța c = | F 1 F 2 | 2 F_ | >>> se numește distanța focală.
• Cantitatea e = c a = 1 # x2212; b 2 a 2> = >>>>>> se numește excentricitate.
• Diametrul unei elipse se numește o coardă arbitrară care trece prin centrul său. Diametrele conjugate ale unei elipse sunt numite perechea diametrelor sale, care au următoarea proprietate: mijlocul acordurilor paralele cu primul diametru se află pe cel de-al doilea diametru. În acest caz, mijlocul acordurilor paralele cu al doilea diametru se află pe primul diametru.
• Raza elipsei la un anumit punct este segmentul care conectează centrul elipsei cu punctul și, de asemenea, lungimea sa, care se calculează cu formula r = a b b 2 cos 2 # x2061; # x03C6; + a 2 sin 2 # x2061; # x03C6; = b 1 # x2212; e 2 cos 2 # x2061; # x03C6; \ cos ^ \ varphi + a ^ \ sin ^ \ varphi >>> = \ cos ^ \ varphi >>>>. unde # x03C6; - unghiul dintre raza și axa semimajor.
• Parametrul focal p = b 2 a >>> este jumătatea lungimii coardei. trecând prin focalizare și perpendicular pe axa majoră a elipsei.
• Raportul dintre lungimile semiaxelor mici și mari se numește coeficientul de comprimare al elipsei sau al elipticității. k = b a.>.> Valoarea egală cu (1 # x2212; k) = a # x2212; b a.>,> se numește contracția unei elipse. Pentru un cerc, raportul de compresie este egal cu unitatea, iar contracția este zero. Coeficientul de compresie și excentricitatea elipsei sunt legate de relația k 2 = 1 # x2212; e2 = 1-e ^>
• Pentru fiecare dintre focare există o linie numită directrix. astfel încât raportul distanței de la un punct arbitrar al elipsei la focalizarea sa la distanța de la acest punct la o linie dată este egal cu excentricitatea elipsei. Întreaga elipsă se află pe aceeași parte a liniei drepte ca și focalizarea. Ecuațiile direcției elipse în forma canonică sunt scrise cu x = # x00B1; p e (1 + e) ​​>> pentru focare ( # x2213; p 1 + e. 0)>, \, 0 \ right)> respectiv. Distanța dintre focalizare și director este p e.>.>

Relația dintre elementele elipsei [ ]

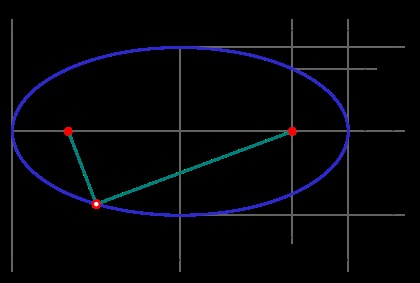
Părți ale elipsei (pentru o descriere, consultați "Definiții înrudite")

Elipsa ca o curbă a ordinii a doua [ ]

Elipsa este o curbă centrală non-degenerată de ordinul doi și satisface o ecuație generală a formei

un 11 x 2 + a 22 y 2 + a 12 x 2 y 2 + a 13 x 2 + a 23 + a 33 y = 0. x ^ + ^ a_y + 2a_xy + 2a_x + 2a_y + a_ = 0,>

Relația dintre invarianții curbei celei de-a doua ordini și semiaxele elipsei (este adevărată numai cu condiția ca centrul elipsei să coincidă cu originea și a 33 = # x2212; 1 = -1>):

Dacă rescriem ecuația generală în formă

A X 2 + B X Y + C Y 2 + D X + E Y + F = 0. + BXY + CY ^ + DX + EY + F = 0,>

atunci coordonatele centrului elipsei sunt:

Unghiul de rotație este determinat din exprimare

Direcțiile vectorilor de axe:

Lungimile semiaxelor sunt date de expresii

Raportul Reverse - coeficienți generali de ecuații ale parametrilor elipsă - poate fi obținută prin substituirea ecuației canonice (vezi mai jos). Expresia rotirea sistemului de coordonate de către un unghi Θ și transfer la punctul (x c y c.), Y _)>:

x # x2032; 2 a 2 + y # x2032; 2 b 2 = 1 >>> + >>> = 1> x # x2032; = (x # x2212; x c) c o s # x0398; + (y # x2212; y c) s i n # x0398; ) cos \ Theta + (y-y_) sin \ Theta> y # x2032; = # x2212; (x # x2212; x c) s i n # x0398; + (y # x2212; y c) c o s # x0398; ) sin \ Theta + (y-y_) cos \ Theta>

Efectuând substituția și deschizând parantezele, obținem următoarele expresii pentru coeficienții ecuației generale:

A = a 2 (s i n # x0398; ) 2 + b 2 (c o s # x0398; ) 2 (sin \ Theta) ^ + b ^ (cos \ Theta) ^> B = 2 (b2 # x2212; a 2) s i n # x0398; c o s # x0398; -a ^) sin \ Theta cos \ Theta> C = a 2 (c o s # x0398; ) 2 + b 2 (s i n # x0398; ) 2 (cos \ Theta) ^ + b ^ (sin \ Theta) ^> D = # x2212; 2 A x c # x2212; B y c -By_> E = # x2212; B x c # x2212; 2 C y c-2 C y> F = A x c 2 + C y c 2 + B x c y c # x2212; a 2 b 2 ^ + Cy ^ ^ + Bx_y_-a ^ b ^>

Dacă introduceți numai unghiul și părăsiți centrul elipsei la origine,

Trebuie remarcat faptul că, în ecuația formei generale a unei elipse definit în carteziene sistem de coordonate, coeficienții ABCDE F (sau, echivalent, un 11. 2a 12. 22. 2a 13. 2 33 a 23. a, 2a_, a_, 2a_, 2a_, a_>) sunt definite până la un factor constant arbitrar, adică la intrarea și la

A k X2 + B k X Y + C k Y 2 + D k X + E k Y + F k = 0 + BkXY + CKY ^ + DKX + EKY + Fk = 0>

unde k # x2260; 0. sunt echivalente. Nu se poate aștepta această expresie

va fi executat pentru orice k.

Relația dintre invariantul I și semiaxele în formă generală este după cum urmează:

unde F # x2032; = F # x22C5; (A # x22C5; h 2 + B # x22C5; h # x22C5; k + C # x22C5; k 2 # x2212; 1) + B \ cdot h \ cdot k + C \ cdot k ^ -1)> - raportul F în originea de transfer la centrul elipsei, ecuația se reduce la

Alți invarianți se află în următoarele relații:

Ecuația canonică [ ]

Pentru orice elipsă, găsim un sistem de coordonate carteziene astfel încât elipsa să fie descrisă de ecuația:

Această ecuație se numește ecuația canonică a unei elipse. Descrie o elipsă cu centrul de la origine, ale cărui axuri coincid cu axele coordonatelor. [1]

Pentru caracterul clar, am setat 0

Cunoscând semi-axa elipsei, puteți calcula distanța focală și excentricitatea: