O parabolă este locul punctelor, pentru fiecare dintre acestea distanța până la un anumit punct fix al planului numită focalizare este egală cu distanța către o anumită linie fixă numită directrix. Obiectivul parabolei este notat cu litera F, distanța de la focalizare la direcție este dată de litera p. Numărul p este denumit parabola.
Să fie dată o parabolă. Introducerea sistemului de coordonate cartezian, astfel încât axa x trece prin punctul central al parabolei și perpendicular pe directricea a directricea a fost direcționată către focalizarea; originea este situată în mijloc între focalizare și regizor (figura 19). În acest sistem de coordonate, această parabolă va fi determinată de ecuație
Ecuația (1) se numește ecuația canonică a unei parabole. În același sistem de coordonate, direcția directă a unei parabole date are o ecuație
Raza focală a unui punct arbitrar M (x; y) al unei parabole (adică lungimea segmentului FM) poate fi calculată din
O parabolă are o axă de simetrie, numită axa parabolului, cu care se intersectează la un singur punct. Punct de intersecție al unei parabole
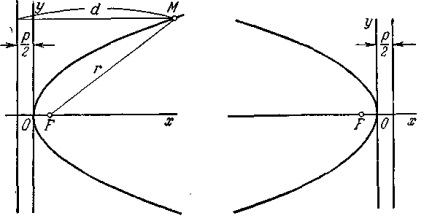
La naiba. 19. La naiba. 20.
cu o axă numită vertex. Cu selecția de mai sus a sistemului de coordonate, axa parabolei este aliniată cu abscisa, vârful este la origine, întreaga parabolă se află în jumătatea dreaptă.
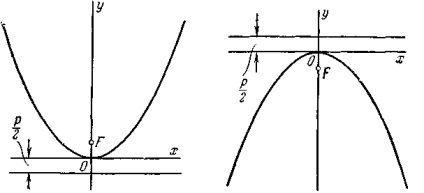
La naiba. 21. La naiba. 22.
Dacă sistemul de coordonate este ales astfel încât axa x este aliniată cu axa parabolei, originea - (. 20 caracteristici) din partea de sus, ci un parabole se află în jumătatea stângă, ecuația lui va fi
În cazul în care originea este la vârf și axa coordonatelor coincide cu axa, parabola va avea o ecuație
dacă se află în jumătatea superioară a planului (figura 21) și
- în jumătatea inferioară a planului (figura 22).
Fiecare dintre ecuațiile parabolei (2), (3), (4), cum ar fi ecuația (1), se numește canonică.
583. Scrieți ecuația unei parabole a cărei vârf este la origine, știind că:
1) parabola este situată în jumătatea dreaptă dreaptă, simetrică pe axa Ox. și parametrul său p = 3;
2) parabola este situată în jumătatea planului stâng, simetric față de axa Ox. și parametrul său p = 0,5;
3) parabola se află în jumătatea superioară superioară, simetrică față de axa Oy. și parametrul său p =;
4) parabola este localizată în jumătatea inferioară a planului, simetrică pe axa Oy. și parametrul său p = 3.
584. Determinați valoarea parametrului și poziția relativă la axele de coordonate ale următoarelor parabole:
585. Scrieți ecuația parabolei a cărei vârf este la origine, știind că:
1) parabola este dispusă simetric în jurul axei Ox și trece prin punctul A (9; 6);
2) parabola este dispusă simetric în jurul axei Ox și trece prin punctul B (- 1; 3);
3) parabola este dispusă simetric în jurul axei Oy și trece prin punctul C (1; 1);
4) parabola este dispusă simetric în jurul axei Oy și trece prin punctul D (4; -8).
586. Un cablu de oțel este suspendat la două capete; Punctele de fixare sunt la aceeași înălțime; distanța dintre ele este egal cu 20 m. Mărimea deflexie la o distanță de 2 m de punctul de fixare, presupunând orizontala este de 14,4 cm. Se determină valoarea jgheabului de cablu în mijloc între punctele de atașare, aproximativ presupunând că cablul are forma unui arc de parabole.
587. Scrieți ecuația parabolică care are focalizarea F (0; -3) și trece prin origine, știind că axa ei este axa Oy.
588. Stabiliți liniile care sunt definite prin următoarele ecuații:
Desenați aceste linii pe desen.
589. Găsiți focalizarea F și ecuația direcției directe a parabolei pentru z = 24x.
590. Calculați raza focală a punctului M al parabolei la z = 20x. Dacă abscisa lui M este 7.
591. Calculați raza focală a punctului M al parabolei la z = 12x. Dacă ordinul punctului M este egal cu 6.
592. Pe parabola la a = 16x găsiți punctele a căror rază focală este de 13.
593. Scrieți ecuația parabola dacă sunt date focalizarea F (-7; 0) și ecuația directrix x -7 = 0.
594. Construiește ecuația parabolică, știind că vârful ei coincide cu punctul (a; 3), parametrul este egal cu p, axa este paralelă cu axa Ox și parabola se extinde până la infinit:
1) în direcția pozitivă a axei Ox;
2) în direcția negativă a axei Ox.
595. Construiți ecuația parabolică, știind că vârful ei coincide cu punctul (a; (3), parametrul este egal cu p, axa este paralelă cu axa Oy și parabola se extinde până la infinit:
1) în direcția pozitivă a axei Oy (adică parabola se înalță);
2) în direcția negativă a axei Oy (adică parabola este în jos).
596. Pentru a stabili că fiecare din următoarele ecuații determină o parabolă și găsiți coordonatele vârfului său A, valoarea parametrului p și ecuația directoarei:
597. Setați că fiecare dintre următoarele ecuații definește o parabolă și găsiți coordonatele vârfului A și valoarea parametrului p:
698. Stabiliți că fiecare din următoarele ecuații definește o parabolă și găsiți coordonatele vârfului său A și valoarea parametrului p:
599. Determinați ce linii sunt definite prin următoarele ecuații:
Desenați aceste linii pe desen.
600. Scrieți ecuația parabola dacă focalizarea ei este F (7; 2) și directrix x = 5 = 0.
601. Scrieți ecuația parabola dacă focalizarea ei este F (4; 3) și directrix y + 1 = 0.
602. Scrieți ecuația parabola dacă focalizarea ei este F (2; -1) și directrix x-y-1 = 0.
603. Având în vedere vârful parabolei A (6; -3) și ecuația direcției sale directe
Găsiți focalizarea F a acestei parabole.
604. Având în vedere vârful parabolei A (-2; -1) și ecuația direcției sale directe
Scrieți ecuația acestei parabole.
605. Determinați punctele de intersecție a liniei x + y - 3 = 0 și parabola x 2 = 4y.
606. Stabiliți punctele de intersecție a liniei 3x + 4y-12 = 0 și parabola y 2 = -9x.
607. Determinați punctele de intersecție a liniei 3x - 2y + 6 = 0 și parabola y 2 = 6x.
608. În următoarele cazuri, determinați modul în care linia dată este relativă la o anumită parabolă - fie intersectează, atinge sau extinde în afara ei:
609. Determinați pentru care valori ale coeficientului unghiular k
linia dreaptă y = Axa + 2:
1) intersectează parabola pentru z = 4x;
3) trece dincolo de această parabolă.
610. Derulați condiția sub care linia y = kx + b este tangentă la parabola y 2 = 2px.
611. Dovada ca la o parabolă la z = 2px se poate desena o singură tangentă cu un coeficient unghiular k ≠ 0.
613. Scrieți ecuația liniei drepte, care este tangentă la parabola în z = 8x și paralelă cu linia
614. Scrieți ecuația unei linii drepte care atinge parabola x 2 = 16y și este perpendiculară pe linia dreaptă
615. Desenați o tangentă la parabolă la z = 12x paralel cu linia dreaptă
și se calculează distanța d între această tangență și linia dată.
616. Pe parabola la z = 64x, găsiți punctul M1 cel mai apropiat de linie
și se calculează distanța d de la punctul M1 la această linie.
617. Scrieți ecuațiile tangentelor la parabolă la z = 36x. trase din punctul A (2; 9).
618. A fost trasă o linie tangentă la parabola lui z = 2px. Dovada că vârful acestei parabole se află în mijlocul punctului de intersecție a tangentei cu axa Ox și proiecția punctului de tangență pe axa Ox.
619. Din punctul A (5; 9), sunt trase tangente la parabola y 2 = 5x. Scrieți ecuația coardei care conectează punctele de tangență.
620. Din punctul P (-3; 12), tangenteaza la parabola
Calculați distanța d de la punctul P la coarda parabolului care leagă punctele de tangență.
621. Determinați punctele de intersecție a elipsei parabolei în z = 24x.
622. Determinați punctele de intersecție ale hiperboliei
și parabola pentru z = 3x.
623. Determinați punctele de intersecție a două parabole:
624. Pentru a dovedi că linia referitoare la parabolei într-un punct M este unghiuri egale cu raza punctului focal M și cu un fascicul care, de M, este paralelă cu axa parabolei în direcția în care parabolei se extinde la nesfârșit.
625. Din centrul unei parabole
La un unghi ascuțit, o rază de lumină este îndreptată spre axa Ox. Se știe că 3 tgα =. După ce a ajuns la parabolă, sa reflectat fasciculul. compune
ecuația liniei pe care se află raza reflectată.
626. Dovadați că două parabole care au o axă comună și o focalizare comună situată între vârfurile lor se intersectează într-un unghi drept.
627. Să se demonstreze că dacă două parabole cu axe reciproc perpendiculare se intersectează la patru puncte, atunci aceste puncte se află pe un cerc.
Articole similare
Trimiteți-le prietenilor: