Binomul lui Newton și triunghiul lui Pascal

Blaise Pascal (1623-1662).

Isaac Newton (1643-1727).
De fapt, nu există nimic de temut. Binom teorema - formula arbitrară grad de descompunere naturală \ binom ((a + b) ^ n \) într-un polinom. Fiecare dintre noi cunosc prin formula de inima „sumă pătrat» \ ((a + b) ^ 2 \) și „sumă cub» \ ((a + b) ^ 3 \), dar creșterea exponentul pentru a determina coeficienții termenilor de start polinomul dificultăți. Pentru a nu face o greșeală și a aplica formula binomică Newton:
Într-o formă mai generală, formula pentru coeficienții din binomial este scrisă după cum urmează:
unde k este numărul ordinal al termenului în polinom.
Să ne amintim că factorialul - produsul numerelor naturale de la 1 la n, atunci \ (1 * 2 * 3 * \ ldots * n \) - notat n, de exemplu, \ (4 = 1 * 2 * 3 * 4 = 24! \).
Amintiți-vă că formula este foarte dificilă. Dar vom încerca să o analizăm. Este evident că orice polinom conține n și b n cu coeficienți 1. Este de asemenea clar că orice alt membru al polinomului arata ca produsul unui anumit grad de fiecare dintre termenii binomului (a + b), în plus, suma gradelor este întotdeauna egal cu n. De exemplu, expresia \ [(a + b) ^ 3 = a ^ 3 + 3a ^ 2b + 3ab ^ 2 + b ^ 3 \] suma gradelor factorilor în toate termeni egali la trei (3, 2 + 1, 1 + 2, 3). Același lucru este valabil și pentru orice alt grad. Singura întrebare este ce coeficienți trebuie utilizați pentru membri.
Se pare că, pentru a facilita activitatea de cercetători și studenți, marele matematician și fizician francez Blaise Pascal acum trei sute cincizeci de ani a inventat un instrument special pentru a identifica cele mai multe dintre acesti factori - „triunghiul lui Pascal“.
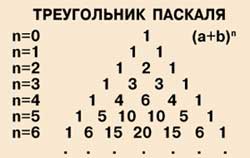
Acesta este construit după cum urmează obrazom.V unitate triunghi vertex scriere 1 corespunde expresiei \ ((a + b) ^ 0, \), pentru că orice număr ridicat la puterea de la zero, dă unitate. Completând triunghiul, notăm mai jos. Acest coeficienți de dilatare ai aceluiași binom ridicat la primul grad: \ (. (A + b) ^ 1 = a + b \) Du-te înainte. latură a triunghiului de unități, și între ele formând - suma a două dintre cele care sunt pe partea de sus, adică, 2. Acesta este coeficienții trinomial „sumă pătrat“:
Următoarea serie, precum și cea anterioară, începe și se termină cu unitățile, iar între ele - cantitatea de numere care sunt de mai sus: 1, 3, 3, 1. Avem suma coeficientilor de cub descompunere“. Mai mulți coeficienți binomiali patra putere va fi de 1, 4, 6, 4, 1, și așa mai departe.
De exemplu, folosind triunghiul Pascal, extindem polinomul într-o sumă de binomială în a șasea putere:
\ [(A + b) ^ 6 = a ^ 6 + 6a ^ 5b + 15a ^ 4b ^ 2 + 20a ^ 3b ^ 3 + 15a ^ 2b ^ 4 + 6ab ^ 5 + b ^ 6. \]
Totul este foarte simplu și memorabil pentru viață. Apropo, independent de a aminti și de a deduce formula de Newton binom, desenat pe un triunghi Pascal, mult mai ușor.
Articole similare
Trimiteți-le prietenilor: