Stea și accelerația unui corp rotativ

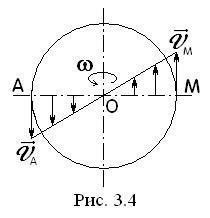
1. Vitezele de puncte ale corpului. Considerăm un punct M dintr-un corp rigid situat la o distanță h de axa de rotație (vezi figura 9). Când corpul se rotește, punctul M va descrie un cerc de rază h. a cărui plan este perpendicular pe axa de rotație, iar centrul C se află pe axa însăși. Dacă rotația elementară a corpului prin unghiul dφ are loc în timpul dt, atunci punctul M realizează deplasarea elementară ds = hdφ de-a lungul traiectoriei sale. Apoi valoarea numerică a vitezei punctului va fi egală cu raportul ds la dt,







Viteza, spre deosebire de viteza unghiulară a corpului, este uneori numită viteza liniară sau circumferențială a punctului M.

Astfel, valoarea numerică a vitezei unui punct al unui corp rigid rotativ este egală cu produsul vitezei unghiulare a corpului prin distanța de la acest punct la axa de rotație.

Este îndreptată viteza de-a lungul tangentei către punctul circumscris al cercului sau perpendiculară pe planul care trece prin axa de rotație și punctul M.

Deoarece pentru toate punctele corpului are aceeași valoare într-o anumită clipă, vitezele punctelor corpului rotativ sunt proporționale cu distanțele lor față de axa de rotație.

Viteza și accelerarea punctului corpului rotativ

În consecință, viteza liniară a oricărui punct al corpului rotativ este egală cu produsul vitezei unghiulare prin distanța de la punctul dat la axa de rotație. Această viteză este întotdeauna îndreptată de-a lungul tangentei către cerc, pe care acest punct o descrie în timpul mișcării sale.

Stea și accelerația unui corp rotativ
La fiecare moment dat, vitezele unghiulare ale punctelor corpului rotativ sunt egale. Prin urmare, vitezele liniare ale punctelor corpului sunt proporționale cu distanța față de axă (fig.3.4), adică rata variază de la o lege polinomică.







T

Stea și accelerația unui corp rotativ
ak ca punct din corp face miscare curbilinie (puncte de traiectorie - cercul) atunci suma totală a accelerației normale și accelerații tangențiale kotoryeopredelyayutsya,

,

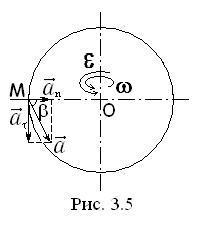
Astfel, accelerația completă a punctului va fi (3.15). Rezultă din (3.15) că accelerația totală a punctului corpului rotativ este proporțională cu distanța față de axa de rotație.

Când mișcarea de rotație a corpului în jurul unei axe normale de accelerare este numită și centripetă (vector este îndreptat radial spre centrul de curbură), și se face referire la accelerare ca tangențială altfel - accelerația de rotație (vectorul accelerație este direcționat de-a lungul tangentei).

47. Viteza și accelerarea unui punct sub metoda vectorului pentru stabilirea mișcării

C

Stea și accelerația unui corp rotativ
scurtarea unui punct este o cantitate care caracterizează cât de repede și în ce direcție se schimbă poziția unui punct în spațiu. Deoarece determină direcția de deplasare a punctului, viteza este o valoare a vectorului. Să presupunem că în timpul Δt vectorul de rază al punctului M sa schimbat cu valoarea Δ. Apoi, viteza medie este cantitatea vectorului (2.1)

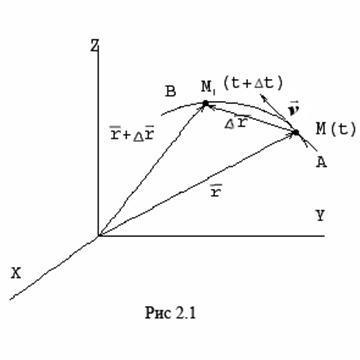
Acest vector este direcționat în același mod ca și. Valoarea limită, atunci când tinde la zero, va determina valoarea instantanee a vitezei la o anumită clipă de timp

Deoarece coarda MM1 tinde la zero. și, prin urmare, vectorul se rotește în jurul punctului M, apropiindu-se de tangenta la traiectoria de la punctul M și în limita care coincide cu ea. Prin urmare, vectorul este direcționat de-a lungul tangentei la traiectoria punctului în direcția mișcării.

În cazul general al mișcării curbilinii, vectorul de viteză se schimbă în magnitudine și direcție în funcție de timp. În consecință, în timp vectorul poate fi reprezentat în formă. Accelerarea punctului din mișcarea curbilinie caracterizează rapiditatea variației vectorului în magnitudine și direcție. Apoi se determină valoarea medie a accelerației și valoarea instantanee sau







Articole similare

Pagina anterioară

Pagina următoare

Trimiteți-le prietenilor: