Scurtă descriere a documentului:
Exemplul următor se referă la aplicarea conceptului de derivat pentru rezolvarea problemelor geometrice. Pentru aceasta, conceptul de tangent este mai întâi dezvăluit. Pe planul de coordonate este afișat un grafic al funcției, pe care sunt marcate două puncte M și S. O linie dreaptă este trasă prin punctele marcate. Acesta arată modul în care în punctul S se apropie de punctul M al liniei drepte poziția de conectare se apropie de poziția tangentei la punctul M. tangent reprezintă o poziție limită a secantă prin două puncte generate în timpul punctele de apropiere. După introducerea conceptului de tangent, considerăm tangenta graficului funcției y = f (x) la punctul M (a, f (a)). Este necesar să găsiți panta tangentei. Pentru aceasta, la o anumită distanță față de M, este marcat punctul N (a + δx, f (a + δx)). Panta liniei este tangenta unghiului la care se află linia care conține ipotenuza triunghiului format de incrementul argumentului și funcția increment bH AU. Corespunzător, panta secantului este dată de formula ks = δy / δx. Ca punctele δx → 0 abordare. Este evident că coeficientul tangentei în abordarea punctelor este determinat de poziția limită a secantului la δx → 0, kkas = lim ksec. sau kkas. = lim δu / δх.
Concluziile din particularitățile modelului matematic pentru rezolvarea ambelor probleme sunt formulate sub forma unei definiții a derivatului unei funcții, descoperirea căreia apare în probleme. Se remarcă faptul că, pentru o y funcție = f (x), definit la punctul x și vecinătatea acesteia, limita DU / bH la bH → 0 este derivata y = f (x) la acel moment. Se introduce notația derivatului f '(x). Pentru materialul de absorbție este considerat un derivat al unei funcții liniare - se remarcă faptul că, deoarece anterior gasit pentru functia y = kx + m limita lim DU / bH la bH = k → 0, y „= (kx + m)“ = k. De asemenea, limita găsită a funcției y = x 3. egală cu lim δω / δх = 3х 2 pentru δx → 0 înseamnă că derivatul y '= (x 3)' = 3x2.
Semnificația fizică și geometrică a derivatului este dezvăluită. Se remarcă faptul că în sensul fizic pentru legea mișcării rectiliniare s (t) derivatul înseamnă viteza instantanee v = s '(t). În sens geometric pentru tangent. efectuată la punctul x = a la graficul funcției y = f (x), derivatul f '(a) este panta tangentei.
Având în vedere semnificația derivatului și formula sa pentru a găsi lim AU / bH = f „(x) la bH → 0, există aproape direct proporțional cu funcția increment a creșterii argumentului cu coeficient care reprezintă δu≈f derivat“ (x) · bH. Astfel, pentru derivata funcției y = x 3 δu≈3h true 2 raport · bH.
Un algoritm este dat pentru găsirea derivatului unei funcții, în care este necesară:
- În punctul x, găsiți f (x);
- Când treceți la punctul x + δx, găsiți f (x + δx);
- Găsiți incrementul funcției f (x + δx) - f (x);
- Scrieți un raport δy / δx;
- Găsiți lim δy / δx pentru δx → 0, adică, f '(x).
Conform acestui algoritm, se dau exemple de definiție a derivatului funcțiilor f (x) = C, unde (C) '= 0; f (x) = 1 / x, unde (1 / x) '= - 1 / x 2.
Se dezvăluie conceptul de diferențiere a unei funcții, adică găsirea derivatului său. Se remarcă faptul că funcția este diferențiată la un punct dacă are un derivat în ea și de asemenea diferențiabilitatea unei funcții la un punct indică continuitatea unei funcții în ea și conversația este falsă. Un exemplu de confirmare a acestei afirmații este constatarea derivatului y = | x | la punctul x = 0. Se remarcă faptul că, în ciuda continuității funcției în acest punct, nu poate exista o tangență a graficului în ea. Deci, nu există nici un derivat în acest moment. Această ieșire este afișată separat pe ecran și este recomandată pentru stocare. Un exemplu de afirmație este o funcție y = f (x), care pe x<0 равна -√-х, а на промежутке x>= 0 este egal cu √ x. Figura prezintă un grafic al funcției pe care este vizibilă continuitatea funcției. Cu toate acestea, la punctul x = 0, tangenta graficului nu poate fi construita, deci nu exista nici un derivat in acest punct. Se reamintește că dacă o tangentă nu poate fi construită la un moment dat în graficul funcției sau este perpendiculară pe abscisă, funcția nu este diferențiată. În acest exemplu, funcția nu este diferențiată. Un grafic arbitrar al unei funcții din ultimul exemplu consideră diferențiabilitatea sa la trei puncte.

Să luăm în considerare două probleme diferite, fizice și geometrice, care vor duce la apariția unui nou model matematic.
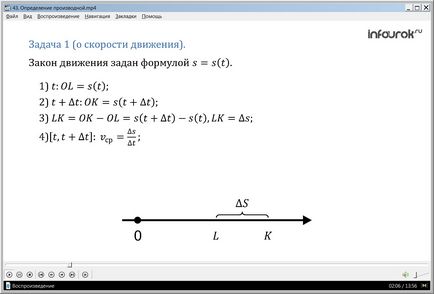
Sarcina 1 (privind viteza de mișcare). Pe linia dreaptă, pe care este dată originea, unitatea de măsură (metru) și direcția, un corp (punct material) se mișcă. Legea mișcării definită prin formula s = s (t) (es es egale te), unde t - timp (secunde), s (t) - poziția corpului pe linia dreaptă (coordonate se deplasează punct material) la momentul t în raport cu partea de sus numărare (în metri). Găsiți viteza corpului la momentul t (în m / s).
Soluția. Să presupunem că în momentul în care corpul era în punctul respectiv
L (fig.1), după traversarea căii de la începutul mișcării OL = s (t). Dăm argumentul t
Creșterea δt (delta te) și luați în considerare timpul t + δt. Coordonarea punctului material a devenit diferită, corpul în acest moment va fi în punctul K: OK = s (t + t) (aproximativ egal cu es plus te delta te).
Astfel, în secunde t corpul sa mutat de la punctul L la punctul K, adică calea LK a trecut. Avem: LK = OK-OL = s (t + t) -s (t). Diferența rezultată se numește incrementarea funcției: s (t + t) -s (t) = s. Astfel, LK = s (metri).
Calea (metri) a corpului a trecut în t secunde. Nu este dificil să găsim viteza medie de mișcare a corpului în intervalul de timp [t, t + t]: vcp. = (m / s) (viteza medie este egală cu raportul dintre delta și delta te).
Și care este viteza v (t) la momentul t (uneori numită viteză instantanee)? Putem spune: aceasta este viteza medie de deplasare pentru un interval de timp [t, t + t], cu condiția ca t să devină mai mici și mai mici; cu alte cuvinte, cu conditia ca t0. Asta înseamnă că
v (t) = (ee din te este limita vitezei medii) și
Rezumând soluția problemei 1, obținem:
Pentru a rezolva următoarea problemă, trebuie să aflăm ce se înțelege prin tangenta la curbă.
Având o curbă L (Figura 2), se selectează punctul M. Se ia un punct mai mult pe curbă, care este suficient de aproape de M, punctul S.
Desenăm MS secant. Apoi aproximăm punctul S de-a lungul curbei L la
punctul M. MS-ul de securitate își va schimba poziția, se pare că se rotește în jurul punctului M. Deseori se întâmplă să găsim o linie dreaptă în acest proces, care este o anumită poziție limită a secantului; Această linie dreaptă - poziția limită a secantului - este numită
tangentă la curba L la punctul M.
Problema 2 (pe tangenta graficului unei functii). Se dă un grafic al funcției y = f (x). Pe acesta este aleasă punctul M (a; f (a)) (em cu coordonatele a și ef de la a). În acest moment, o linie tangentă este trasă la graficul funcției (presupunem că există).
Găsiți panta tangentei.
Soluția. Să dăm argumentul o incrementare x și să luăm în considerare pe grafic (figura 3) punctul N cu abscisa a + x. Ordonata lui N este f (a + x). Coeficientul unghiular al secvenței MN. și anume tangenta unghiului dintre secant și axa x. se calculează cu formula (secantul este egal cu jocul delta împărțit la delta X).
Dacă acum avem tendința x la zero, atunci punctul N începe să se apropie de curbă până la punctul M. Tangenta pe care am caracterizat-o
Ca poziție limitativă a secantului în această aproximare. Prin urmare, este normal să presupunem că panta kkac tangente va fi calculată prin formula (tangenta este egală cu limita k-secantului).
Folosind formula de mai sus pentru ks. obținem: (tangenta este egală cu limita deltei delta împărțită de delta X, deoarece delta X tinde la zero).
Să rezumăm. În procesul de rezolvare a două probleme, am ajuns la același model matematic - raportul dintre creșterea funcției și incrementarea argumentului, atunci când creșterea argumentului tinde la zero.
Să analizăm care este limita raportului dintre creșterea incrementului unei funcții și creșterea incrementului unui argument.
2. Definiția derivatului
Definiție 1. Fie o funcție y = f (x) definită la un anumit punct x și într-o zonă vecină a acesteia. Dăm argumentul x o creștere de x, astfel încât să nu părăsească vecinătatea indicată. Să găsim incrementul corespunzător al funcției δy și să formăm o relație. Dacă există o limită a acestei relații în condiția x0, atunci această limită este numită derivatul funcției y = f (x) la punctul x și denotă f '(x) (primul lui x).
Deci, (delta delta limită, împărțită prin delta X, este egală cu prima lui X).
Pentru a desemna derivatul, este adesea folosit simbolul y '. (accident vascular cerebral)
Menționăm că y „= f“ (x) (y bar este bara de ef al X) - este o caracteristică nouă, dar asociată cu funcția y = f (x), definit în toate punctele de astfel de x, în care există peste limita de . Această funcție este numită după cum urmează: derivata funcției y = f (x).
În exemplul pentru funcția liniară y = kx + m, egalitatea rămâne.
Aceasta înseamnă că y '= k sau, mai în detaliu,
Am demonstrat că pentru funcția y = x 3 avem egalitatea
Aceasta înseamnă că y '= 3x2 sau, mai în detaliu, (x3)' = 3x2 (în cub, prime este egal cu trei X în a doua putere)
Derivat din punct de vedere fizic și geometric.
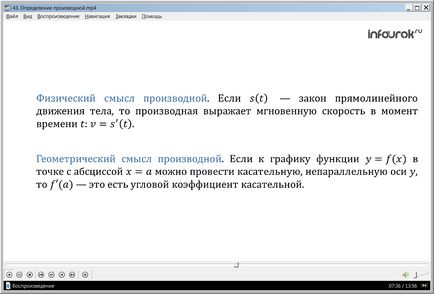
Sensul fizic (mecanic) al derivatului este următorul. Dacă s (t) este legea mișcării rectilinii a corpului, atunci derivatul exprimă viteza instantanee la momentul t:
v = s '(t) (ee este egal cu prime de te).
Semnificația geometrică a derivatului este după cum urmează. Dacă graficul funcției y = f (x) la punctul cu abscisa x = a se poate face o tangentă neparalele axa y, f „(a) există un coeficient unghiular tangențial.
Fie funcția y = f (x) un derivat la un anumit punct x: (limita raportului dintre incrementul funcției și incrementul argumentului este egală cu derivatul funcției).
Obținem: într-o vecinătate suficient de mică a punctului x, o egalitate aproximativă este îndeplinită: (raportul incrementului funcției cu incrementul argumentului este aproximativ egal cu derivatul funcției) sau
y f '(x) x. (incrementarea funcției este aproximativ egală cu derivatul funcției înmulțit cu creșterea argumentului).
Creșterea funcției este "aproape proporțională" cu creșterea argumentului, coeficientul de proporționalitate fiind valoarea derivată (la un anumit punct x). De exemplu, pentru funcția y = x 3, egalitatea aproximativă y 3x 2 · x
Să formulăm algoritmul pentru găsirea derivatului.
Algoritmul de căutare pentru derivat (pentru funcția y = f (x))
1. Fixați valoarea lui x, găsiți f (x).
2. Dați argumentul x o creștere de x, mergeți la un punct nou
x + x, găsiți f (x + x).
3. Gasiti cresterea functiei: y = f (x + x) -f (x).
4. Desenați o relație.
5. Calculați limita.
Această limită este f '(x).
Exemplul 1. Găsiți derivatul unei funcții constante y = C.
Soluția. Folosim algoritmul pentru găsirea derivatului.
1) Pentru o valoare fixă de x, avem f (x) = C.
2) La punctul x + x avem: f (x + x) = C.
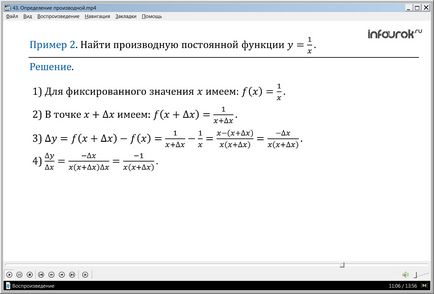
Exemplul 2. Găsiți derivatul funcției y =.
Soluția. Folosim algoritmul pentru găsirea derivatului.
Dacă funcția y = f (x) are un derivat la punctul x, atunci el se numește diferențiabil la punctul x. Găsirea derivatului funcției y = f (x) se numește diferențierea funcției y = f (x).
Dacă funcția este diferențiată la punctul x, atunci este și ea continuă în acest punct.
Contraversul este fals.
Dăm exemple: funcția y = | x | este continuă peste tot și la punctul x = 0 (Figura 4), dar nu există o tangență la graficul funcției la "punctul de joncțiune" (0; 0).
Dacă o tangentă nu poate fi trasă la un anumit punct la graficul funcției, atunci nu există derivat în acest punct.
Un exemplu. În Fig. 5 prezintă graficul funcției piesei y = f (x), unde
Funcția este continuă pe linia întregului număr, inclusiv la punctul x = 0. Și tangenta la graficul funcției există în orice punct, inclusiv la punctul x = 0. Dar la punctul x = 0 tangenta coincide cu axa y, adica, este perpendiculară pe axa abscisei, ecuația lui are forma x = 0. Această linie dreaptă nu are un coeficient unghiular, prin urmare, nu există f '(0).
Pentru a trage o concluzie cu privire la diferențiabilitatea unei funcții, este necesar să verificăm dacă este posibilă trasarea unei tangente la un grafic al unei funcții la un punct care nu este perpendicular pe abscisă. Dacă este posibil, atunci în acest moment funcția este diferențiabilă. Dacă la un moment dat tangenta la graficul funcției nu există sau este perpendiculară pe axa abscisă, atunci în acest moment funcția nu este diferențiată. Astfel, conform graficului funcției arătate în Fig. 6, putem concluziona că funcția este continuă peste tot cu excepția punctului x = a; funcția este diferențiată peste tot, cu excepția punctelor x = a, x = b - aici nu există tangenta, x = c - linia tangentă este paralelă cu axa y.
Trimiteți-le prietenilor: