observații V ≈ 0.
Astfel, vizibilitatea se modifică periodic în ceea ce privește z
modelul meu de difracție. Motivul acestor schimbări în diferența defazări de trei valuri plane care călătoresc în z> 0 din zăbrele: val axial deplasare de-a lungul axei z. și două valuri laterale care se deplasează în direcția sin α = ± Ω / k = ± λ / d.
2.2.2. Difracția pe o fază sinusoidală de fază
Funcția de transmisie (a se vedea (3.5)):
t (x) = eim cos Ω x.
Presupunem că adâncimea de modulare a fazei este mică, adică m 1. Apoi
t (x) ≈ 1 + im cosx = 1 + im 2 e i Ω x + im 2 e - i Ω x.
Atunci când această rețea este iluminată de un val incident incident normal, amplitudinile a se află în spatele zăbrelei (pentru z> 0)
f (x, z) = ae ikz + iam 2 e i (Ω x + √ k 2 -Ω 2 z) + iam 2 e i (-Ω x + √ k 2 -Ω 2 z).
Comparând cu (3.54), vedem că trei valuri au aceeași amplitudine și aceeași direcție de propagare ca în cazul unei grătare de amplitudine. Diferența se face numai în fazele inițiale: factorul i = e iπ / 2 în al doilea și al doilea
Al treilea termen arată că oscilațiile prin valuri oblice (la origine x = 0 graniță plan z = 0 +), rămase în fază cu π / 2 din oscilațiile axiale ale undei (deplasare în direcția axei z).
2.3. Fresnel difracție pe structuri periodice. Efectul Talbot (auto-reproducere)
Un exemplu de structură periodică este un ecran cu elemente identice dispuse periodic, de exemplu, fante paralele de aceeași lățime b. situate la aceeași distanță d una de cealaltă. Lăsați un astfel de ecran (grilaj) să fie iluminat din stânga printr-un plan incident normal (lungime de undă λ).
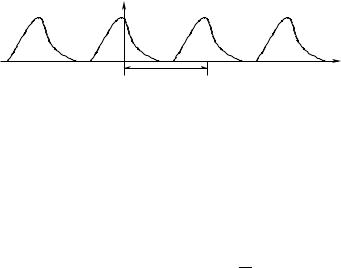
adică avem de-a face cu regiunea de difracție Fresnel.) În acest plan avem φ n = 2πn 2. adică schimbarea de fază relativă a tuturor undelor plane este un multiplu de 2π. Este evident că diferența în raidurile de fază ale oricăror două valuri (cu frecvențe spațiale n 1 2π / d și

182 Difracție. optica Fourier
n 2 2π / d), care este egal cu 2π (n 2 1 - n 2 2). este, de asemenea, un multiplu de 2π. Dar schimbarea diferenței de fază a oscilațiilor cu o sumă care este un multiplu de 2π. nimic nu schimbă suma de
marmură oscilantă. Am găsit un rezultate remarcabile: relația de fază dintre componentele unde plane au fost aceleași atât în planul adiacent grilei (unde suma undelor plane (3,55) au format o limită de câmp f periodice 0 (x)) și
în plan (3.57). Identitatea (într-un multiplu de 2π) a relațiilor de fază a termenilor de valuri plane conduce la faptul că,
că rezultatul interferenței acestor valuri plane este identic, adică câmpul luminos în planul z 1 diferă de câmpul de frontieră f 0 (x) numai de factorul de fază constantă e ikz:
f (x, z 1) = e ikz 1 f 0 (x).
Observăm în planul z 1 o structură periodică care repetă identic câmpul de frontieră f 0 (x). Este, de asemenea, clar că o astfel de revoltă
Imaginea structurii periodice se repetă la distanțe care sunt multipli de z 1:
186 Difracție. optica Fourier
În al doilea rând, fasciculul ar trebui să fie ¾ subțire: amplitudinea și faza valului în secțiunea transversală a fasciculului ar trebui să varieze ușor în timpul trecerii bannerului. Exprimăm această condiție cantitativ. Fie t (x) = a (x) e iφ (x) transmisia complexă a transparenței, unde a (x) este transparența amplitudinii, φ (x) = kLn (x) Diferența de amplitudine și
faza în secțiunea transversală a fasciculului după trecerea transparenței
+ b / 2 în planul z = 0
în Fig. 3.30) va fi
φ ≈ dx b = kLb dx
respectiv. Starea micuței lor
pot fi scrise în formă
Condiția (3.64), împreună cu a doua inegalitate (3.65), dă
Prin urmare, este suficient să se solicite ca grosimea transparenței L
și neomogenitatea indicelui de refracție
2.5.3. Ce este un fascicul de lumină paralelă
Aranjăm pe calea unei valuri plane oblice f (x) = ae ik sin α · x cu o frecvență spațială u 0 = k sin α o distanță de diafragmă de lățime b (Figura 3.31). În planul z = 0 +. adiacente fantei din dreapta, obținem
Astfel, dincolo de decalajul din regiunea z> 0, în loc de zona idealizată
un val valuric al cărui amplitudine de oscilații în toate punctele de pe suprafața undei (și, prin urmare, pentru toate -∞ de la zero), obținem un fascicul paralel de lumină, a cărui direcție (unghiul α) coincide cu direcția incidentului de undă plane de pe diafragma cu fantă, secțiunea transversală a fasciculului este | x | 6 2 b. Este clar că O lumină cu lungime limitată cu lanț ușor nu mai este un val de avion cu o frecvență spațială u 0. Acesta este un pachet de valuri plane care este formată din unde plane cu frecvențe spațiale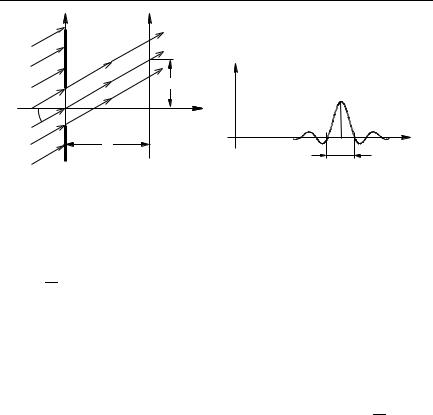
Fig. 3.31. înclinat
Fig. 3,32. spațial
spectrul para-
(C 0 (u) este transformarea Fourier a câmpului f 0 (x), vezi Figura 3.32). Deci, permițând valului avionului să treacă prin diafragma cu lățimea b. obținem un pachet de valuri plane cu o frecvență purtătoare u 0 (frecvența centrală a pachetului) și o frecvență de răspândire | u | 6 2 b π. Rețineți că atunci când diafragma fantei este deplasată în planul z = 0 în sus cu o distanță x 0, obținem spectrul
C 1 (u) = C 0 (u) e - i (u - u 0) x 0.
(Deplasarea funcției f 0 (x) de-a lungul coordonatei x cu o sumă x 0 duce la multiplicarea spectrului său cu factorul de fază liniară e - i (u - u 0) x 0.)
Ce se întâmplă cu pachetul de undă având un spectru spațial C 0 (u) în timpul propagării în z> 0. La o deplasare de fază distanța z pentru pachetul de frecvență purtătoare u este 0 φ 0 ≈ kz - 2 z k u 2 0. Pentru
undele cu o frecvență spațială u 0 +
u (amintesc, ne interesează
u 0 e - iz sin α (u - u 0).
Ultima ecuație înseamnă că forma pachetului de valuri rămâne neschimbată, adică o rază paralelă de lumină care se propagă în planul z. rămâne un fascicul paralel cu o secțiune transversală nemodificată și direcție α. obține doar o schimbare de fază (aceeași ca și pentru o undă plană cu frecvența spațială u 0) și schimbă direcția transversală (de-a lungul axei x) cu valoarea x 0 = z sin α (comparați cu
Dacă condiția (3.63) nu este îndeplinită, atunci există dispersie spațială. faze de raid de diferite valuri plane (diferite
undele de frecvență) care formează un pachet de valuri, se dovedesc a fi diferite, pachetul de unde se răspândește. În particular, la distanțele z b λ 2 (regiunea de difracție Fraunhofer) intervalul de valori de x. unde
amplitudinea oscilațiilor este diferită de zero, este determinată de lățimea maximului principal al modelului de difracție | x | = λ b z b. În acest fel,
termenul "fascicul paralel al luminii" devine lipsit de sens dacă vorbim despre propagarea unui val de secțiune transversală finită | x |
2.6. Câmp în planul focal al obiectivului. Transformarea spațială Fourier
După cum se știe, lentila se concentrează pe un fascicul paralel de lumină: o undă plană care rulează în direcția α (Figura 3.33), adică având o frecvență spațială u = k sin α. focalizează obiectivul în punctul focal
avion cu coordonate
x = f tg α ≈ f sin α =
Există, după cum vedem, o corespondență unu-la-unu între punctele planului focal și frecvențele spațiale ale undelor plane, care sunt focalizate în aceste puncte. Se pare că există și o corespondență unu-la-unu între amplitudinile și fazele oscilațiilor la punctele planului focal și la undele plane corespunzătoare.
Lăsați un val arbitrar să cadă pe obiectiv. În planul de intrare П 1. distanța față de obiectiv la o distanță z. Valul are o amplitudine complexă f 0 (x). Reprezentăm acest val sub forma unei suprapuneri de valuri plane de direcții diferite α n. adică amplitudinea complexă a acestui val
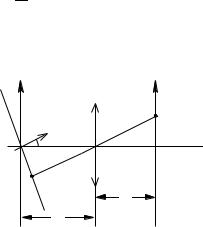
în forma (3.42). Valul de undă c n e iu n x. corespunzător
Nome a componentelor prezentate în Fig. 3.33: vectorul de undă face un unghi α = α n (sin α n = u k n) cu axa optică. Coeficientul c n = a n e iφ n determină amplitudinea undei plane a n și faza inițială φ n (faza oscilației la punctul ξ = 0 planul P 1, la fel și faza de oscilație la punctul P 1. situată pe suprafața AA aceeași undă „).
Fig. 3.33. Valul planului este focalizat pe punctul planului focal
Este evident că amplitudinea oscilațiilor la punctul P al planului focal este proporțională cu amplitudinea a n a undelor plane, care în acest moment
M-am concentrat. Vom găsi ceea ce relația de fază între oscilațiile în diferite puncte ale planului focal. Este clar că oscilație la punctul P în spatele fazei de oscilație la punctul P 1 (și, prin urmare, la punctul ξ = 0 planul de intrare), în cazul în care diferența de fază este determinată de lungimea căii optice de P. liniei P 1 P 1 P perpendicular la fiecare punct
suprafețele de undă la suprafețele plane într-un incident de undă pe o lentilă și sferice într-un val care a trecut printr-o lentilă. (Calea optică P 1 P include, de asemenea, o parte a traseului care trece direct în lentilă.) Lăsați întârzierea de fază corespunzătoare căii P 1 P să fie egală cu ψ n. Apoi, faza oscilației la punctul P al planului focal este φ n + ψ n,
iar amplitudinea complexă a oscilațiilor din acest punct poate fi scrisă
forma f (xn) a n e i (φ n + ψ n) = c n e n n.
La termenul c 0 e iu 0 x (pentru u 0 = 0) corespunde o undă plană care se deplasează de-a lungul axei optice (α = 0). Acesta se concentrează originea x = 0 planul focal F. Coeficientul c 0 = a 0 0 e iφ determină amplitudinea acestui val de 0 și faza sa inițială φ 0. r. Faza de E. Oscilația la P O planul de intrare 1. Întârziere faza ψ 0 în punctul x = 0 al planului focal Φ, unde acest val a fost focalizat, este determinat de lungimea OO a căii optice. Amplitudinea complexă a oscilațiilor în acest punct este f (0) a 0 e i (φ 0 + ψ 0)
Pentru a continua descărcarea, trebuie să colectați imaginea:
Articole similare
Trimiteți-le prietenilor: