Cercul. definiții și formule de bază:
Dacă punctul este un punct arbitrar al planului și punctul este un punct fix, atunci =. Apoi - forma vectorială a circumferinței razei. în forma coordonată, ecuația cercului are forma:
Dacă centrul cercului este la origine (0,0), atunci ecuația (1) ia forma cea mai simplă: → ecuația canonică.
Dacă în loc de (1) avem egalitatea :. atunci nu este greu să obțineți expresia :.
În funcție de valoarea E, astfel de cazuri pot fi realizate:
1).> 0. care este → un cerc :.
2). = 0 →. este satisfăcut pentru un punct (x0, y0).
3). <0. то есть → – мнимая окружность .
Exemplul 1-242. Fie centrul cercului, - raza cercului. . . - puncte dintr-un cerc. Desenați o ecuație de cerc în fiecare dintre următoarele cazuri:
1) (2, -3), = 7; 2) (2,6), (-1,2); 3) (3,2), (-1,6) - capetele diametrului cercului; 4) (1, -1), o linie dreaptă. = 0 este tangentă la cerc; 5) (1,2) este punctul unui cerc, cercul este tangent la axele de coordonate; 6) (3,1), (-1,3) - punctele cercului, aparține liniei. = 0; 7) (-1,3), (0,2), (1, -1) sunt punctele cercului.
1). Scrieți imediat ecuația cercului :.
2). Din condiția în care avem: = (2,6) - (-1,2) = (3,4) → = = 5. Apoi ecuația cercului :.
3). Deoarece centrul cercului împarte segmentul dat în jumătate, atunci =. din care: 2 = + = (2.8) → = (1.4). În același timp, = = (-4, -4) → = 2. Apoi ecuația cercului :.
4). Raza cercului este egală cu distanța până la tangent. Normalizăm ecuația unei linii drepte și găsim abaterea unui punct din această linie: = = 2 → = 2. Apoi este ecuația cercului.
5). Să desemnează o rază a unui cerc =. Luând în considerare proprietatea tangențială a cercului axelor de coordonate, scriem ecuația cercului :. Deoarece punctul aparține cercului, este necesar :. Din ecuația obținem două rădăcini: = 1 și = 5. Soluție: sau.
6). Punctele (3,1) și (-1,3) alocă o coardă în cerc. Teorema este cunoscută a fi o linie dreaptă. Trecând prin mijlocul coardei cercului și perpendicular pe el, trece prin centrul acestui cerc.
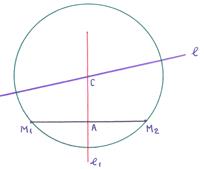
Punctul de intersecție a liniilor drepte și găsirea din sistemul de ecuații: găsim coordonatele centrului (2,4). Radiusul cercului: = = =. Apoi: - ecuația cercului cerut.
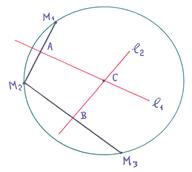
Să găsim ecuația. Din egalitatea vectorilor = avem 2 =. noi găsim. Scrieți =. vom lua = (1, -3). Apoi ecuația. . sau.
Punctul de intersecție a liniilor drepte și găsirea din sistemul de ecuații: → (-4, -1). Radiusul cercului: = = = 5. Apoi: - ecuația cercului cerut.
Elipsă. locusul geometric al punctelor planului, pentru fiecare dintre acestea suma distantelor catre doua puncte date ale planului, numite focare. există o valoare constantă, mare. decât distanța dintre focuri.
Dacă presupunem că semiaxisul este jumătatea majoră, atunci focurile elipsei sunt situate pe axă. și: = - focalizare stângă, = - focalizare dreapta.
Ecuația canonică a elipsei este: - axa semimajor; - axa semimajor. Valoare. . sunt legate de relația: = -.
O caracteristică importantă a unei elipse este cantitatea: - excentricitatea, care determină gradul de comprimare a cercului de-a lungul axei.
Pentru a calcula distanțele față de focare, utilizați expresiile: =. =. și + = 2.
Un loc special în proprietățile elipsei este ocupat de linii drepte: și - direcția directă. Poziția directrix determină numărul :. Desen general pentru elipsă:
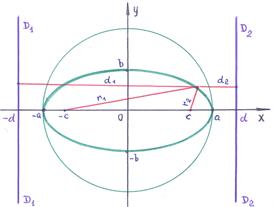
Exemplul 2-249. Stabiliți ecuația b). definește o elipsă. Găsiți centrul său. semiaxele și ecuațiile directrix.
1). Rescriem ecuația dată :. sau este ecuația canonică a elipsei cu centrul.
2). Semiaxisul elipsei: = 5, = 4. Calculăm: = - = 9. Calculam excentricitatea: = =. Calculăm parametrul directrix: = =. Ecuațiile directrix. = -. . = sau. și. .
Răspuns: b) centrul; semiaxis: = 5, = 4; Directoarea. . . .
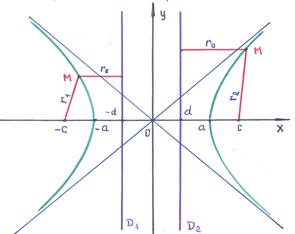
Lăsați punctele focale ale hiperboliei să stea pe axă. și: = - focalizare stângă, = - focalizare dreapta. Ecuația canonică a hiperboliei are forma :. în plus <и . Эксцентриситет гиперболы: . Фокальные расстояния определяются выражениями:
Direcțiile directe ale hiperboliei sunt determinate de parametru. Asimptotele hiperboliei definesc expresiile: = ±.
Notă. pentru aranjamentul presupus al focarelor, axa se numește axa reală a hiperbolei, iar axa se numește axa imaginară.
Exemplul 3 -265. Ecuația de ordinul doi este dată :. Arătați că linia este o hiperbolă, scrieți ecuația canonică. Găsiți: a) semiaxurile, b) coordonatele focarelor, c) excentricitatea, d) ecuațiile directrix și asymptote.
1). Rescriem ecuația: - aceasta este ecuația canonică a hiperbolei cu focare situate pe axă.
2). Axa hiperboliei: = 3, = 4. Calculăm: = + = 25. Aceasta înseamnă: = - focalizare stângă, = - focalizare dreapta. Calculam excentricitatea: = =. Calculăm parametrul directrix: = =. Ecuațiile directrix. = -. . =. Ecuațiile asimptotelor prin expresia: = ± = ±.
Răspunsul este: a) ecuația hiperbola. = 3, = 4; b. focalizează. =; c) excentricitatea =; d) directorii. = -. . =. asimptote: = ±.
Exemplul 4 -269 b). Ecuația de ordinul doi este dată :. Arătați că linia este o hiperbolă, găsiți centrul ei și notați ecuația canonică. Găsiți: semiaxele, coordonatele focarelor, excentricitatea, ecuațiile direcțiilor directe și asimptote.
1). Rescriem ecuația: - o ecuație canonică hiperbola cu focarele aranjate pe o linie dreaptă = 1, cu centrul la (-5.1).
2). Folosim traducerea paralelă a sistemului de coordonate :. . Apoi ecuația ia forma canonică, pentru care toate cantitățile pot fi scrise folosind cele mai simple formule. Axa hiperbola: = 8, = 6. Se calculează: = + = 100. Aceasta înseamnă: = - focalizare stângă, = - focalizare dreapta. Calculam excentricitatea: = =. Calculăm parametrul directrix: = =. Ecuațiile directrix. = -. . =. Ecuațiile asimptotelor prin expresia: = ± = ±.
3). Având în vedere. . scrieți ecuațiile pentru vechiul sistem de coordonate: pentru directrix. = -. . = și pentru asimptote -1 = ±. Focalizează:. =.
Răspuns: ecuația :. = 8, = 6; trucuri =. =; excentricitate =; Directoarea. = -. . =. asimptote: -1 = ±.
Parabola. locusul de puncte pe plan, pentru fiecare dintre care distanța până la un anumit punct al planului, numit focalizare. este egal cu distanța până la o linie dreaptă dată, numită directrix.
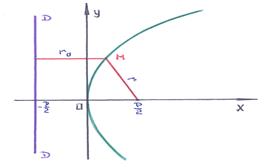
Folosind notația folosită în figură, în conformitate cu definiția acceptată a unei parabole. Ecuația canonică a unei parabole este ușor de obținut. Pentru parabola: -excentricitatea.
Notă. figura și dispunerea directoarei și focalizarea corespund cazului în care axa parabolei este, de asemenea, o axă.
1). Din ecuația: rezultă că axa parabolei este axa. parametrul său. Ramurile parabolei sunt îndreptate spre dreapta.
2). Din ecuația: rezultă că axa parabolei este axa. Avem o parabolă cu parametrul =. Ramurile parabolei sunt îndreptate în sus.
3). Din ecuația: rezultă că axa parabolei este axa. Avem o parabolă cu parametrul = 2, iar graficul parabolei date este graficul parabolei. mapat simetric în raport cu axa. Ramurile parabolei sunt îndreptate spre stânga.
4). Din ecuația: rezultă că axa parabolei este axa. Avem o parabolă cu parametrul =. iar graficul parabolei date este graficul parabolei. mapat simetric în raport cu axa. Ramurile parabolei sunt îndreptate în jos.
Exemplul 6 -288. Pentru a stabili că fiecare ecuație dată: 1); 2); 3) definește o parabolă. Găsiți coordonatele vârfului și parametrul pentru fiecare parabolă.
1). Din ecuația: rezultă că axa parabolei este axa. Avem o parabolă cu parametrul =. Ramurile parabolei sunt îndreptate în jos. Diagrama parabolei date este graficul parabolului. mutat de 2: avem.
2). Din ecuația: rezultă că axa parabolei este axa. Avem o parabolă cu parametrul = 3, ramurile parabolei sunt îndreptate în jos. Diagrama parabolei date este graficul parabolului. a fost schimbat în dreapta cu 6 și în jos cu 1: avem.
3). Din ecuația: rezultă că axa parabolei este axa. Avem o parabolă cu parametrul =. Ramurile parabolei sunt îndreptate spre stânga. Diagrama parabolei date este graficul parabolului. schimbat la stânga cu 4 și mai mare cu 3: avem.
Articole similare
Trimiteți-le prietenilor: